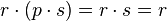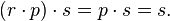Example of a commutative non-associative magma

In mathematics, it can be shown that there exist magmas that are commutative but not associative. A simple example of such a magma is given by considering the children's game of rock, paper, scissors.

A commutative non-associative magma

Karnaugh diagram of all possibilities of the Commutative, Associative, Inverse, and Identity law to hold (y) or not to hold (n), and the definition of an according binary operation ⊕ on the integers for almost each possibility.

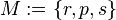Let $M := \{ r, p, s \}$ and consider the binary operation 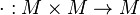$\cdot : M \times M \to M$ defined, loosely inspired by the rock-paper-scissors game, as follows:

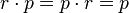r \cdot p = p \cdot r = p

"paper beats rock";

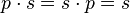p \cdot s = s \cdot p = s

"scissors beat paper";

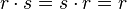r \cdot s = s \cdot r = r

"rock beats scissors";

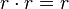r \cdot r = r

"rock ties with rock";

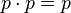p \cdot p = p

"paper ties with paper";

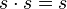s \cdot s = s

"scissors tie with scissors".

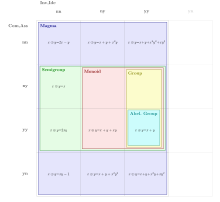
The last three equations show the additional property of idempotence of such magma, whose Cayley table results to be:

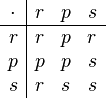
$\begin{array}{c|ccc} \cdot & r & p & s\\ \hline r & r & p & r\\ p & p & p & s\\ s & r & s & s \end{array}$

By definition, the magma 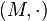$(M, \cdot)$ is commutative, but it is also non-associative, as the following shows:

r \cdot (p \cdot s) = r \cdot s = r

but

(r \cdot p) \cdot s = p \cdot s = s.

See the bottom row in the picture for more example operations, defined on the integer numbers.

A commutative non-associative algebra

Using the above example, one can construct a commutative non-associative algebra over a field $K$ : take $A$ to be the three-dimensional vector space over $K$ whose elements are written in the form

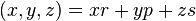(x, y, z) = x r + y p + z s

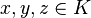for $x, y, z \in K$ . Vector addition and scalar multiplication are defined component-wise, and vectors are multiplied using the above rules for multiplying the elements 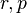$r, p$ and $s$ . The set

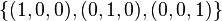\{ (1, 0, 0), (0, 1, 0), (0, 0, 1) \}

i.e.

\{ r, p, s \}

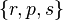
forms a basis for the algebra $A$ . As before, vector multiplication in $A$ is commutative, but not associative.