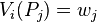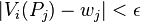Exact division

An exact division (also called: even division) is a kind of fair division in which a resource is divided among two or more partners with subjective valuations, such that all partners agree that every partner received exactly his due proportion of the resource.^[1]

If all the weights are equal to 1/n, then the division is also called a perfect division.^[2] For example, consider a land asset that has to be divided among 3 heirs: Alice and Bob who think that it's worth 3 million dollars, and George who thinks that it's worth $4.5M. In a perfect division, all three heirs receive a land-plot that Alice and Bob believe to be worth exactly $1M and George believes to be worth exactly $1.5M.

Exact divisions always exist, but they cannot be found by discrete protocols (with a finite number of queries). There is a moving-knife protocol which finds an exact division for two partners. For more than two players, only near exact procedures are known.

Near-exact division procedures are used as sub-routines in other cake-cutting procedures such as the Robertson-Webb protocol for envy-free cake-cutting.

Definition

Let 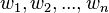$w_1, w_2, ..., w_n$ be n weights representing the different entitlements of the n partners (i.e. partner i is entitled to a fraction 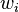$w_i$ of the cake). Assume that the sum of all weights is 1 and that all partners value the cake C as 1.

An exact division in the ratios 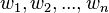$w_1, w_2, ..., w_n$ is a partition of the cake to n pieces: $C = P_1 \sqcup ... \sqcup P_n$ , such that for every partner i and every piece j:

V_i(P_j)=w_j

I.e., all partners agree that every partner j received exactly his due share of 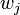$w_j$ .^[1]

Near-exact division

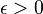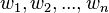For every $\epsilon>0$ , An $\epsilon$ -near-exact division in the ratios $w_1, w_2, ..., w_n$ is a division in which:

|V_i(P_j)-w_j| < \epsilon

I.e., all partners agree that every partner j received nearly-exactly his due share of 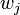$w_j$ , where the difference is less than $\epsilon$ .^[1]

Existence

When the value functions are additive and non-atomic, an exact division exists for every set of weights. This is a consequence of the convexity of the space of partitions.^[3]^[4]

Both the necklace splitting problem and a generalization of the ham sandwich theorem from measure theory can be used to establish existence proofs for exact divisions in various circumstances.^[5]

Exact division procedures

Moving-knife procedure

Austin moving-knife procedure produces a division of the cake in which each of the n partners receives a piece that he values as exactly 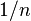$1/n$ . When there are only 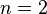$n=2$ partners, this division is exact, since each partner necessarily believes that both pieces are worth exactly 1/2. But when 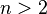$n>2$ this is not the case.

In fact, as of 2015, there is no known generalization of this moving-knife procedure to more than 2 partners. There are

Piecewise-Constant procedure

A value measure on a certain resource is called piecewise constant if the resource can be partitioned to a finite number of convex pieces, such that the value density in every piece is constant. For example, consider a circular cake in which each of its 4 quarters has a different topping. A person that values each of the toppings differently (but does not distinguish between different pieces having the same topping) has a piecewise constant valuation.

If the value measures of all partners are piecewise constant, then the resource can be partitioned to a finite number of convex sub-pieces such that in each sub-piece the value densities of all partners are constant. It is possible to divide each of these sub-piece to n parts of equal size and give each person 1/n of each sub-piece. This division is perfect - all partners agree that the values of all pieces are 1/n.

This algorithm can be generalized to slightly more general families of value measures, such as piecewise linear.^[2]

Near-Exact division procedures

Crumb-and-Pack procedure

For any given 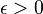$\epsilon > 0$ , one can give each partner a piece such that all partners believe that the values they have differ by less than $\epsilon$ , i.e., for every i and every j:^[1]

|V_i(P_j)-w_j| < \epsilon

The near-exact division procedure has two steps: crumbing and packing.

Crumbing step: the goal is to cut the cake to tiny bits ("crumbs") such that each partner assigns a sufficiently small value to each crumb. This is done in the following way. Let k be a certain constant. Ask partner #1 cut the cake to k pieces that he values as 1/k. Ask partner #2 to trim pieces as needed (using at most k-1 cuts) such that each piece has a value of at most 1/k. These new pieces of course still have a value of at most 1/k for partner #1. Continue with partners #3, #4, ..., #n. Finally all n partners value each resulting crumb as at most 1/k.

Packing step: the goal here is to partition the crumbs to n subsets, such that the sum of values in each subset j is near w_j. Here is an intuitive explanation of the packing step for two partners (Alice and George) when the weights are 1/2.^[6]

Get an empty bowl.
Insert into the bowl one of the crumbs.
If the value in the bowl becomes more than 1/2 to either partner, give the bowl to that partner and give the other crumbs to the other partner.
Otherwise (the value in the bowl is less than 1/2 to both partners), if the value in the bowl is larger for Alice than for George, then find a crumb whose value for George is more than its value for Alice (such a crumb must exist because the sum of values of all crumbs is 1 both for Alice and for George). Add this crumb to the bowl and return to step 2.

It is possible to prove by induction, that the difference in the valuation of the bowl between Alice and George is always at most 1/k. Hence, when one of the partners receives the bowl, its value for both partners is between than 1/2-1/k and 1/2+1/k.

Formally, each piece can be represented as a vector of values, one per partner. The length of each vector is bounded, i.e. for each such vector v: 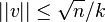$||v||\leq \sqrt{n}/k$ . Our goal is to create, for each partner j, a vector all whose elements are near w_j. To do this, we have to divide the vectors to subsets, such that the sum of vectors in each subset j is sufficiently close to a vector all whose elements are w_j. This is possible thanks to a theorem by V.Bergström,^[7]^[8]

The Crumb-and-Pack procedure is a subroutine in the Robertson-Webb protocol. The latter protocol generates a division which is both near-exact and envy-free.

A different explanation of the crumb-and-pack procedure is provided by Brams and Taylor.^[9]

Truthful mechanisms

Any algorithm for perfect division relies on the value measures reported by the partners. If the partners know how the algorithm works, they may have an incentive to lie about their value measures in order to receive more than 1/n. In order to prevent this, incentive compatible (truthful) mechanisms can be used.^[2]^[10]

The simplest truthful division mechanism is: select a single partner at random and give him the entire cake. This mechanism is trivially truthful because it asks no questions. Moreover, it is perfect in expectation: the expected value of each partner is 1/n according to all value measures. However, the resulting division is of course not perfect and even not proportional.

A better truthful mechanism for perfect division can be built given any existing algorithm (or oracle) for finding a perfect division:

Ask each partner to report his value measure.
Use the existing algorithm/oracle to generate a partition which is perfect according to the value functions reported by the partners, i.e., each of the n pieces has a value of exactly 1/n to all partners according to their reported valuations.
Perform a random permutation on the perfect partition and give each partner one of the pieces.

Here, the expected value of each partner is still 1/n regardless of the reported value function, so the mechanism is still truthful - no partner can gain anything from lying. Moreover, a truthful partner is guaranteed a value of exactly 1/n with probability 1 (not only in expectation). Hence the partners have an incentive to reveal their true value functions.

Consensus halving

Exact divisions are much easier if the participants cooperate in establishing entitlements rather than competing as in fair division. Some authors refer to this as consensus division or consensus halving.^[11]

A constructive way to divide a resource in two parts with n cuts so all of n people think the halves are of equal was established in 2003.^[12] This consensus halving theorem uses the Borsuk–Ulam theorem and Tucker's lemma and the n cuts is the minimum possible.

Impossibility

It is impossible to achieve an exact division with a finite number of queries, even if there are only 2 partners and the weights are exactly 1/2.^[13] This means that the best we can achieve using a discrete algorithm is a near-exact division.

Proof: When the protocol is at step k, it has a collection of at most k pieces. To provide an exact division, the protocol must find an exact subset - a subset of the pieces which both partners value as exactly 1/2. We are going to prove that, for every k, there are situations in which at step k there is no exact subset, and hence the protocol might have to continue endlessly.

Initially, there is only one piece which both partners value as 1, so there is obviously no exact subset. After one step, at most one partner (say, Alice) has had an option to cut the cake. Even if Alice cuts the cake to two pieces that are equal in her opinion, they may be different in George's opinion, so again there is no exact subset.

Suppose now that we are at step k and there are k pieces. Without loss of generality, we may assume that each piece has a non-zero value to both partners. This is because, if Alice (for example) cuts a piece which she values as 0, it is possible that George also values the same piece as 0, so we can discard this piece and continue with the other pieces.

The total number of different subsets now is 2^k, and by the induction assumption none of them is exact. At step k, the protocol can ask either Alice or George to cut a certain piece to two pieces. Suppose w.l.o.g. that the cutter is George and that he cuts piece X to two sub-pieces: X1 and X2. Now, the total number of subsets is 2^k+1: half of them already existed and by assumption they are not exact, so the protocol's only chance of finding an exact subset is to look at the new subsets. Each new subset is made of an old subset in which the piece X has been replaced with either X1 or X2. Since George is the cutter, he can cut in a way which makes one of these subsets an exact subset for him (e.g. if a certain subset containing piece X had a value of 3/4, George can cut X such that X1 has a value of 1/4 in his opinion, so that the new subset has a value of exactly 1/2). But, George does not know Alice's valuation and cannot take it into account when cutting. Therefore, there is an uncountable infinity of different values that the pieces X1 and X2 can have for Alice. Since the number of new subsets is finite, there is an infinite number of cases in which no new subset has a value of 1/2 for Alice, hence no new subset is exact.

Comparison with other criteria

A perfect division is, in particular, also proportional, envy-free and equitable.

However, it is not necessarily Pareto efficient, since in many cases it is possible to take advantage of the subjective valuations and divide the resources such that all partners receive more than their fair share of 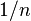$1/n$ .

References

↑ 1.0 1.1 1.2 1.3 Robertson, Jack; Webb, William (1998). Cake-Cutting Algorithms: Be Fair If You Can. Natick, Massachusetts: A. K. Peters. p. 127. ISBN 1568810768.
↑ 2.0 2.1 2.2 Chen, Yiling; Lai, John K.; Parkes, David C.; Procaccia, Ariel D. (2013). "Truth, justice, and cake cutting". Games and Economic Behavior 77 (1): 284–297. doi:10.1016/j.geb.2012.10.009.
↑ Neyman, J (1946). "Un théorèm dʼexistence". C. R. Acad. Sci. 222: 843–845.
↑ Dubins, Lester Eli; Spanier, Edwin Henry (1961). "How to Cut a Cake Fairly". The American Mathematical Monthly 68: 1. doi:10.2307/2311357. JSTOR 2311357.
↑ B. Grünbaum (1960). "Partitions of mass–distributions and convex bodies by hyperplanes". Pacific J. Math 10: 1257–1261.
↑ Adapted from Robertson, Jack; Webb, William (1998). Cake-Cutting Algorithms: Be Fair If You Can. Natick, Massachusetts: A. K. Peters. pp. 68–71. ISBN 1568810768.
↑ V. Bergström (1930). "Zwei Sätze über ebene Vectorpolygone". Hamburgische Abhandlungen 8: 205–219.
↑ Robertson, Jack; Webb, William (1998). Cake-Cutting Algorithms: Be Fair If You Can. Natick, Massachusetts: A. K. Peters. pp. 126–128. ISBN 1568810768.
↑ Brams, Steven J.; Taylor, Alan D. Fair Division [From cake-cutting to dispute resolution]. pp. 131–133. ISBN 0521556449.
↑ Mossel, Elchanan; Tamuz, Omer (2010). "Truthful Fair Division". Lecture Notes in Computer Science: 288–299. doi:10.1007/978-3-642-16170-4_25.
↑ de Longueville, Mark; Živaljević, Rade T. (2008). "Splitting multidimensional necklaces". Advances in Mathematics 218: 926–939. doi:10.1016/j.aim.2008.02.003.
↑ Simmons, Forest W.; Su, Francis Edward (2003). "Consensus-halving via theorems of Borsuk-Ulam and Tucker". Mathematical Social Sciences 45: 15–25. doi:10.1016/S0165-4896(02)00087-2.
↑ Robertson, Jack; Webb, William (1998). Cake-Cutting Algorithms: Be Fair If You Can. Natick, Massachusetts: A. K. Peters. pp. 103–104. ISBN 1568810768.