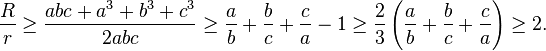Euler's theorem in geometry
In geometry, Euler's theorem states that the distance d between the circumcentre and incentre of a triangle can be expressed as[1][2][3][4]
where R and r denote the circumradius and inradius respectively (the radii of the above two circles). The theorem is named for Leonhard Euler, who published it in 1767.[5] However, the same result was published earlier by William Chapple in 1746.[6]
From the theorem follows the Euler inequality:[2][3]
which holds with equality only in the equilateral case.[7]:p. 198
Proof

Letting O be the circumcentre of triangle ABC, and I be its incentre, the extension of AI intersects the circumcircle at L. Then L is the midpoint of arc BC. Join LO and extend it so that it intersects the circumcircle at M. From I construct a perpendicular to AB, and let D be its foot, so ID = r. It is not difficult to prove that triangle ADI is similar to triangle MBL, so ID / BL = AI / ML, i.e. ID × ML = AI × BL. Therefore 2Rr = AI × BL. Join BI. Because
- ∠ BIL = ∠ A / 2 + ∠ ABC / 2,
- ∠ IBL = ∠ ABC / 2 + ∠ CBL = ∠ ABC / 2 + ∠ A / 2,
we have ∠ BIL = ∠ IBL, so BL = IL, and AI × IL = 2Rr. Extend OI so that it intersects the circumcircle at P and Q; then PI × QI = AI × IL = 2Rr, so (R + d)(R − d) = 2Rr, i.e. d2 = R(R − 2r).
Stronger version of the inequality
A stronger version[7]:p. 198 is
See also
- Fuss' theorem for the relation among the same three variables in bicentric quadrilaterals
References
- ↑ Johnson, Roger A. (2007) [1929], Advanced Euclidean Geometry, Dover Publ., p. 186.
- ↑ 2.0 2.1 Alsina, Claudi; Nelsen, Roger (2009), When Less is More: Visualizing Basic Inequalities, Dolciani Mathematical Expositions 36, Mathematical Association of America, p. 56, ISBN 9780883853429.
- ↑ 3.0 3.1 Debnath, Lokenath (2010), The Legacy of Leonhard Euler: A Tricentennial Tribute, World Scientific, p. 124, ISBN 9781848165250.
- ↑ Dunham, William (2007), The Genius of Euler: Reflections on his Life and Work, Spectrum Series 2, Mathematical Association of America, p. 300, ISBN 9780883855584.
- ↑ Euler, Leonhard (1767), "Solutio facilis problematum quorumdam geometricorum difficillimorum", Novi Commentarii academiae scientiarum Petropolitanae (in Latin) 11: 103–123.
- ↑ Chapple, William (1746), "An essay on the properties of triangles inscribed in and circumscribed about two given circles", Miscellanea Curiosa Mathematica 4: 117–124. The formula for the distance is near the bottom of p.123.
- ↑ 7.0 7.1 Svrtan, Dragutin; Veljan, Darko (2012), "Non-Euclidean versions of some classical triangle inequalities", Forum Geometricorum 12: 197–209.