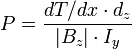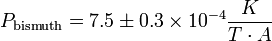Ettingshausen effect

The Ettingshausen Effect (named for Albert von Ettingshausen) is a thermoelectric (or thermomagnetic) phenomenon that affects the electric current in a conductor when a magnetic field is present.[1]

Ettingshausen and his PhD student Walther Nernst were studying the Hall effect in bismuth, and noticed an unexpected perpendicular current flow when one side of the sample was heated. This is also known as the Nernst effect. Conversely, when applying a current (along the y-axis) and a perpendicular magnetic field (along the z-axis) a temperature gradient appears along the x-axis. Because of the Hall effect, electrons are forced to move perpendicular to the applied current. Due to the accumulation of electrons on one side of the sample, the number of collisions increases and a heating of the material occurs. This effect is quantified by the Ettingshausen coefficient P, which is defined as:

P=\frac{dT/dx\cdot d_z}{|B_z|\cdot I_y}

where dT/dx is the temperature gradient that results from the y-component Iy of an electric current and the z-component Bz of a magnetic field. It also depends on the thickness dz of the material because the total heat flow will depend on its cross section for the temperature gradient. P is independent of the sample width because the total Hall voltage will be constant, as will the total drop in T.

temperature gradient due to Ettingshausen effect with applied magnetic field and electric current

In most metals like copper, silver and gold P is on the order of 10−16 K/TA and thus difficult to observe in common magnetic fields. In bismuth the Ettingshausen coefficient is several orders of magnitude larger because of its poor thermal conductivity.

P_{\mathrm{bismuth}}=7.5\pm0.3\times 10^{-4}\frac{K}{T\cdot A}[2]

See also

References

  1. ↑ v. Ettingshausen, A.; Nernst, W. (1886). "Ueber das Auftreten electromotorischer Kräfte in Metallplatten, welche von einem Wärmestrome durchflossen werden und sich im magnetischen Felde befinden". Annalen der Physik und Chemie 265 (10): 343–347. Bibcode:1886AnP...265..343E. doi:10.1002/andp.18862651010. Retrieved 23 February 2012.
  2. ↑ "ettingshausen effect in bismuth" (PDF). Retrieved 3 May 2012.