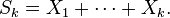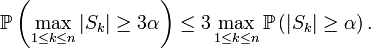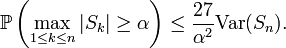Etemadi's inequality
In probability theory, Etemadi's inequality is a so-called "maximal inequality", an inequality that gives a bound on the probability that the partial sums of a finite collection of independent random variables exceed some specified bound. The result is due to Nasrollah Etemadi.
Statement of the inequality
Let X1, ..., Xn be independent real-valued random variables defined on some common probability space, and let α ≥ 0. Let Sk denote the partial sum
Then
Remark
Suppose that the random variables Xk have common expected value zero. Apply Chebyshev's inequality to the right-hand side of Etemadi's inequality and replace α by α / 3. The result is Kolmogorov's inequality with an extra factor of 27 on the right-hand side: