Estrada index

In chemical graph theory, the Estrada index is a topological index of protein folding. The index was first defined by Ernesto Estrada as a measure of the degree of folding of a protein,[1] which is represented as a path-graph weighted by the dihedral or torsional angles of the protein backbone. This index of degree of folding has found multiple applications in the study of protein functions and protein-ligand interactions.

The name of this index as the “Estrada index” was proposed by de la Peña et al. in 2007.[2]

Derivation

Let 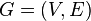G=(V,E) be a graph of size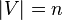|V|=n and let \lambda _1 \geq \lambda _2 \geq ... \geq \lambda _n be a non-increasing ordering of the eigenvalues of its adjacency matrix A . The Estrada index is defined as

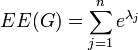
EE(G)=\sum_{j=1}^n e^{\lambda _j}

For a general graph, the index can be obtained as the sum of the subgraph centralities of all nodes in the graph. The subgraph centrality of node 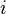i is defined as[3]

EE(i)=\sum_{k=0}^{\infty} \frac{(A^k)_{ii}} {k!}

The subgraph centrality has the following closed form[3]

EE(i)=(e^A)_{ii}=\sum_{j=1}^{n}[\varphi(i)]^2 e^{\lambda _j}

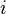where \varphi _j (i) is the i th entry of the 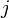jth eigenvector associated with the eigenvalue 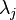\lambda _j . It is straightforward to realise that[3]

EE(G)=tr(e^A)

References

  1. ↑ Estrada, E. (2000). "Characterization of 3D molecular structure". Chem. Phys. Lett. (319): 713. Bibcode:2000CPL...319..713E. doi:10.1016/S0009-2614(00)00158-5.
  2. ↑ de la Peña, J. A.; Gutman, I.; Rada, J. (2007). "Estimating the Estrada index". Linear Algebra Appl. 427: 70–76. doi:10.1016/j.laa.2007.06.020.
  3. ↑ 3.0 3.1 3.2 Estrada, E.; Rodríguez-Velázquez, J.A. (2005). "Subgraph centrality in complex networks". Phys. Rev. E 71 (5): 056103. doi:10.1103/PhysRevE.71.056103.