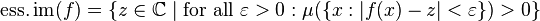Essential range

In mathematics, particularly measure theory, the essential range of a function is intuitively the 'non-negligible' range of the function: It does not change between two functions that are equal almost everywhere. One way of thinking of the essential range of a function is the set on which the range of the function is most 'concentrated'. The essential range can be defined for measurable real or complex-valued functions on a measure space.

Formal definition

Let f be a Borel-measurable, complex-valued function defined on a measure space 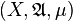$(X,\mathfrak{A},\mu)$ . Then the essential range of f is defined to be the set:

\operatorname{ess.im}(f) = \left\{z \in \mathbb{C} \mid \text{for all}\ \varepsilon > 0: \mu(\{x : |f(x) - z| < \varepsilon\}) > 0\right\}

In other words: The essential range of a complex-valued function is the set of all complex numbers z such that the inverse image of each ε-neighbourhood of z under f has positive measure.

Properties

The essential range of a measurable function is always closed.
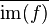The essential range ess.im(f) of a measurable function is always a subset of $\overline{\operatorname{im}(f)}$ .
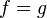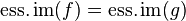The essential image cannot be used to distinguished functions that are almost everywhere equal: If $f=g$ holds $\mu$ -almost everywhere, then $\operatorname{ess.im}(f)=\operatorname{ess.im}(g)$ .
These two facts characterise the essential image: It is the biggest set contained in the closures of 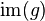$\operatorname{im}(g)$ for all g that are a.e. equal to f:

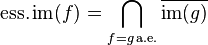\operatorname{ess.im}(f) = \bigcap_{f=g\,\text{a.e.}} \overline{\operatorname{im}(g)}

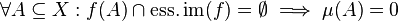The essential range satisfies $\forall A\subseteq X: f(A) \cap \operatorname{ess.im}(f) = \emptyset \implies \mu(A) = 0$ .
This fact characterises the essential image: It is the smallest closed subset of 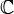$\mathbb{C}$ with this property.
The essential supremum of a real valued function equals the supremum of its essential image and the essential infimum equals the infimum of its essential range. Consequently a function is essentially bounded if and only if its essential range is bounded.
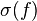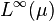The essential range of an essentially bounded function f is equal to the spectrum $\sigma(f)$ where f is considered as an element of the C*-algebra $L^\infty(\mu)$ .

Examples

If $\mu$ is the zero measure, then the essential image of all measurable functions is empty.
This also illustrates that even though the essential range of a function is a subset of the closure of the range of that function, equality of the two sets need not hold.
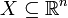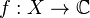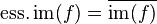If $X\subseteq\mathbb{R}^n$ is open, $f:X\to\mathbb{C}$ and $\mu$ the Lebesgue measure, then $\operatorname{ess.im}(f)=\overline{\operatorname{im}(f)}$ holds. This holds more generally for all Borel measures that assign non-zero measure to every non-empty open set.

References

Walter Rudin (1974). Real and Complex Analysis (2nd edition ed.). McGraw-Hill. ISBN 978-0-07-054234-1.

Essential range

Formal definition

Properties

Examples

See also

References