Ernst angle

In magnetic resonance imaging, the Ernst angle is the flip angle (a.k.a. "tip" or "nutation" angle) for a particular spin that gives the maximal signal in the least amount of time, when signal averaging over many transients. This relationship was developed by Richard R. Ernst, winner of the 1991 Nobel Prize in Chemistry.^[1] ^[2]

The following equation relates the Ernst angle, 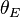$\theta_E$ , to the experimental interpulse delay, d₁; the duration of the Free induction decay, aka "acquisition time", or "a_t"; and the longitudinal relaxation time of the spin in question, T₁:

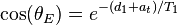
$\cos(\theta_E)=e^{-(d_1+a_t)/T_1}$

For example, if one wishes to get the best signal from a resonance with T₁=3 sec, and one wishes to use d₁= 1sec and a_t=2 sec, the optimal tip angle is 68 degrees.

This relationship is especially important in Magnetic Resonance Imaging (MRI), where interscan delays (d₁) and acquisition times (a_t) are often short relative to the signal's T₁ value. In MRI, there is typically just the resonance of hydrogen being observed and the T₁ of hydrogen depends on its local environment. Note that d₁ and a_t together may be referred to collectively as T_R in the MRI community.

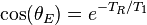
$\cos(\theta_E)=e^{-T_R/T_1}$

From which it is trivial to see that the Ernst angle is

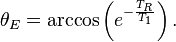
$\theta_E=\arccos\left(e^{-\frac{T_R}{T_1}}\right).$

References

↑ "1991 Nobel Laureates in Chemistry".
↑ Ernst, R. R. (1966). "Application of Fourier transform spectroscopy to magnetic resonance". Review of Scientific Instruments 37: 93. Bibcode:1966RScI...37...93E. doi:10.1063/1.1719961.