Erdős–Hajnal conjecture
In graph theory, a branch of mathematics, the Erdős–Hajnal conjecture states that families of graphs defined by forbidden induced subgraphs have either large cliques or large independent sets.
More precisely, for an arbitrary undirected graph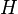 
, let 
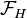be the family of graphs that do not have 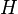as an induced subgraph. Then, according to the conjecture, there exists a constant 
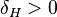such that the 
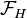-vertex graphs in have either a clique or an independent set of size 
.
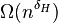In contrast, for random graphs in the Erdős–Rényi model with edge probability 1/2, both the maximum clique and the maximum independent set are much smaller: their size is proportional to the logarithm of , rather than growing polynomially. Ramsey's theorem proves that no graph has both its maximum clique size and maximum independent set size smaller than logarithmic.
This conjecture is due to Paul Erdős and András Hajnal, who proved it to be true when 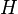is a cograph. They also showed, for arbitrary H, that the size of the largest clique or independent set grows superlogarithmically. As of 2014, however, the full conjecture has not been proven, and remains an open problem.
References
- Alon, Noga; Pach, János; Solymosi, József (2001), "Ramsey-type theorems with forbidden subgraphs", Combinatorica 21 (2): 155–170, doi:10.1007/s004930100016, MR 1832443, Zbl 0989.05124.
- Chudnovsky, Maria (2014), "The Erdös–Hajnal conjecture—a survey", Journal of Graph Theory 75 (2): 178–190, doi:10.1002/jgt.21730, MR 3150572, Zbl 1280.05086.
- Erdős, P.; Hajnal, A. (1989), "Ramsey-type theorems", Discrete Applied Mathematics 25 (1-2): 37–52, doi:10.1016/0166-218X(89)90045-0, MR 1031262, Zbl 0715.05052.