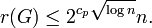Erdős–Burr conjecture
In mathematics, the Erdős–Burr conjecture is an unsolved problem concerning the Ramsey number of sparse graphs. The conjecture is named after Paul Erdős and Stefan Burr, and is one of many conjectures named after Erdős; it states that the Ramsey number of graphs in any sparse family of graphs should grow linearly in the number of vertices of the graph.
Definitions
If G is an undirected graph, then the degeneracy of G is the minimum number p such that every subgraph of G contains a vertex of degree p or smaller. A graph with degeneracy p is called p-degenerate. Equivalently, a p-degenerate graph is a graph that can be reduced to the empty graph by repeatedly removing a vertex of degree p or smaller.
It follows from Ramsey's theorem that for any graph G there exists a least integer
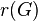, the Ramsey number of G, such that any complete graph on at least 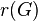vertices whose edges are coloured red or blue contains a monochromatic copy of G. For instance, the Ramsey number of a triangle is 6: no matter how the edges of a complete graph on six vertices are colored red or blue, there is always either a red triangle or a blue triangle.
The conjecture
In 1973, Paul Erdős and Stefan Burr made the following conjecture:
- For every integer p there exists a constant cp so that any p-degenerate graph G on n vertices has Ramsey number at most cp n.
That is, if an n-vertex graph G is p-degenerate, then a monochromatic copy of G should exist in every two-edge-colored complete graph on cp n vertices.
Known results
Although the full conjecture has not been proven, it has been settled in some special cases. It was proven for bounded-degree graphs by Chvátal et al. (1983); their proof led to a very high value of cp, and improvements to this constant were made by Eaton (1998) and Graham, Rödl & Rucínski (2000). More generally, the conjecture is known to be true for p-arrangeable graphs, which includes graphs with bounded maximum degree, planar graphs and graphs that do not contain a subdivision of Kp.[1] It is also known for subdivided graphs, graphs in which no two adjacent vertices have degree greater than two.[2]
For arbitrary graphs, the Ramsey number is known to be bounded by a function that grows only slightly superlinearly. Specifically, Fox & Sudakov (2009) showed that there exists a constant cp such that, for any p-degenerate n-vertex graph G,
Notes
References
- Alon, Noga (1994), "Subdivided graphs have linear Ramsey numbers", Journal of Graph Theory 18 (4): 343–347, doi:10.1002/jgt.3190180406, MR 1277513.
- Burr, Stefan A.; Erdős, Paul (1975), "On the magnitude of generalized Ramsey numbers for graphs", Infinite and finite sets (Colloq., Keszthely, 1973; dedicated to P. Erdős on his 60th birthday), Vol. 1, Colloq. Math. Soc. János Bolyai 10, Amsterdam: North-Holland, pp. 214–240, MR 0371701.
- Chen, Guantao; Schelp, Richard H. (1993), "Graphs with linearly bounded Ramsey numbers", Journal of Combinatorial Theory, Series B 57 (1): 138–149, doi:10.1006/jctb.1993.1012, MR 1198403.
- Chvátal, Václav; Rödl, Vojtěch; Szemerédi, Endre; Trotter, William T., Jr. (1983), "The Ramsey number of a graph with bounded maximum degree", Journal of Combinatorial Theory, Series B 34 (3): 239–243, doi:10.1016/0095-8956(83)90037-0, MR 0714447.
- Eaton, Nancy (1998), "Ramsey numbers for sparse graphs", Discrete Mathematics 185 (1–3): 63–75, doi:10.1016/S0012-365X(97)00184-2, MR 1614289.
- Fox, Jacob; Sudakov, Benny (2009), "Two remarks on the Burr–Erdős conjecture", European Journal of Combinatorics 30 (7): 1630–1645, doi:10.1016/j.ejc.2009.03.004, MR 2548655.
- Graham, Ronald; Rödl, Vojtěch; Rucínski, Andrzej (2000), "On graphs with linear Ramsey numbers", Journal of Graph Theory 35 (3): 176–192, doi:10.1002/1097-0118(200011)35:3<176::AID-JGT3>3.0.CO;2-C, MR 1788033.
- Graham, Ronald; Rödl, Vojtěch; Rucínski, Andrzej (2001), "Paul Erdős and his mathematics (Budapest, 1999)", Combinatorica 21 (2): 199–209, doi:10.1007/s004930100018, MR 1832445
|chapter=ignored (help) - Li, Yusheng; Rousseau, Cecil C.; Soltés, Ľubomír (1997), "Ramsey linear families and generalized subdivided graphs", Discrete Mathematics 170 (1–3): 269–275, doi:10.1016/S0012-365X(96)00311-1, MR 1452956.
- Rödl, Vojtěch; Thomas, Robin (1991), "Arrangeability and clique subdivisions", in Graham, Ronald; Nešetřil, Jaroslav, The Mathematics of Paul Erdős, II, Springer-Verlag, pp. 236–239, MR 1425217.