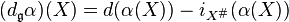Equivariant differential form
In differential geometry, an equivariant differential form on a manifold M acted by a Lie group G is a polynomial map
from the Lie algebra 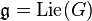 to the space of differential forms on M that is equivariant; i.e.,
to the space of differential forms on M that is equivariant; i.e.,
In other words, an equivariant differential form is an invariant element of
For an equivariant differential form  , the equivariant exterior derivative
, the equivariant exterior derivative 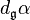 of
of  is defined by
is defined by
where d is the usual exterior derivative and 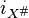 is the interior product by the fundamental vector field generated by X.
It is easy to see
is the interior product by the fundamental vector field generated by X.
It is easy to see 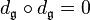 (use the fact the Lie derivative of
(use the fact the Lie derivative of 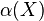 along
along 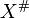 is zero) and one then puts
is zero) and one then puts
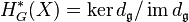 ,
,
which is called the equivariant cohomology of M (which coincides with the ordinary equivariant cohomology defined in terms of Borel construction.) The definition is due to H. Cartan. The notion has an application to the equivariant index theory.
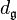 -closed or
-closed or 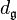 -exact forms are called equivariantly closed or equivariantly exact.
-exact forms are called equivariantly closed or equivariantly exact.
The integral of an equivariantly closed form may be evaluated from its restriction to the fixed point by means of the localization formula.
References
- ↑ Proof: with
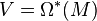 , we have:
, we have: 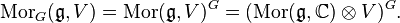 Note
Note ![\mathbb{C}[\mathfrak{g}]](../I/m/98e908f22b08a120f698985cc710868f.png) is the ring of polynomials in linear functionals of
is the ring of polynomials in linear functionals of  ; see ring of polynomial functions.
; see ring of polynomial functions.
- Berline, Nicole; Getzler, E.; Vergne, Michèle (2004), Heat Kernels and Dirac Operators, Berlin, New York: Springer-Verlag
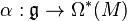
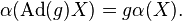
![\mathbb{C}[\mathfrak{g}] \otimes \Omega^*(M) = \operatorname{Sym}(\mathfrak{g}^*) \otimes \Omega^*(M).](../I/m/5f5bf1de0da5426f162c614c6c04c45a.png)