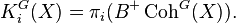Equivariant K-theory

For the topological equivariant K-theory, see topological K-theory.

In mathematics, the equivariant algebraic K-theory is an algebraic K-theory associated to the category 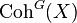\operatorname{Coh}^G(X) of equivariant coherent sheaves on an algebraic scheme X with action of a linear algebraic group G, via Quillen's Q-construction; thus, by definition,

K_i^G(X) = \pi_i(B^+ \operatorname{Coh}^G(X)).

In particular, 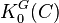K_0^G(C) is the Grothendieck group of 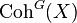\operatorname{Coh}^G(X). The theory was developed by R. W. Thomason in 1980s.[1] Specifically, he proved equivariant analogs of fundamental theorems such as the localization theorem.

Equivalently, 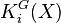K_i^G(X) may be defined as the 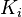K_i of the category of coherent sheaves on the quotient stack [X/G]. (Hence, the equivariant K-theory is a specific case of the K-theory of a stack.)

A version of the Lefschetz fixed point theorem holds in the setting of equivariant (algebraic) K-theory.[2]

Fundamental theorems

Let X be an equivariant algebraic scheme.

Localization theorem — Given a closed immersion 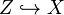Z \hookrightarrow X of equivariant algebraic schemes and an open immersion 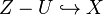Z - U \hookrightarrow X, there is a long exact sequence of groups

\dots \to K^G_i(Z) \to K^G_i(X) \to K^G_i(U) \to K^G_{i-1}(Z) \to \dots

References

  1. ↑ Charles A. Weibel, Robert W. Thomason (1952–1995).
  2. ↑ BFQ 1979

Further reading