Equivalent airspeed

Equivalent airspeed (EAS) is the airspeed at sea level in the International Standard Atmosphere at which the dynamic pressure is the same as the dynamic pressure at the true airspeed (TAS) and altitude at which the aircraft is flying.[1][2] In low-speed flight, it is the speed which would be shown by an airspeed indicator with zero error.[3] It is useful for predicting aircraft handling, aerodynamic loads, stalling etc.

EAS = TAS \times \sqrt{\frac{\rho}{\rho_0}}

Where:

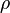\rho\, is actual air density.

\rho_0\, is standard sea level density (1.225 kg/m³ -or- 0.00237 slugs/ft³).

EAS is a function of dynamic pressure.

EAS = \sqrt{\frac{2q}{\rho_0}}

Where:

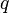{q}\, is dynamic pressure. q = \tfrac12\, \rho\, v^{2},

(this equation requires a consistent system of measurement)

EAS can also be obtained from the aircraft mach number and static pressure.

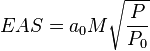
EAS ={a_0} M \sqrt{P\over P_0}

Where:

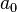{a_0}\, is the standard speed of sound at 15 °C (661.47 knots)

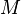M\, is Mach number

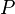P\, is static pressure

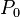P_0\, is standard sea level pressure (1013.25 hPa)

Combining the above with the expression for Mach number gives EAS as a function of impact pressure and static pressure (valid for subsonic flow):

EAS={a_{0}}\sqrt{{5P\over P_{0}}[(\frac{q_c}{P}+1)^\frac{2}{7}-1]}

Where:

{q_c}\, is impact pressure.

At standard sea level EAS is the same as calibrated airspeed (CAS) and true airspeed (TAS). At high altitude, EAS may be obtained from CAS by correcting for compressibility error.

A simplified formula can be used that allows calculation of CAS from EAS.

CAS={EAS\times[1+\frac{1}{8}(1-\delta)M^{2}+\frac{3}{640}(1-10\delta+9\delta^{2})M^{4}]}

where:

Pressure ratio: 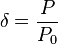\delta=\frac{P}{P_{0}}

CAS\, & EAS\, the airspeeds in either knots, km/h, mph or any other appropriate unit

Above formula is accurate within 1% up to Mach 1.2 and useful with acceptable error up to Mach 1.5. The 4th order Mach term can be neglected for speeds below Mach 0.85.

See also

Notes

  1. ↑ Clancy, L.J. (1975), Aerodynamics, Section 3.8, Pitman Publishing Limited, London. ISBN 0-273-01120-0
  2. ↑ Anderson, John D. (2007), Fundamentals of Aerodynamics, p.215 (4th edition), McGraw-Hill, New York USA. ISBN 978-0-07-295046-5
  3. ↑ Houghton, E.L. and Carpenter, P.W. (1993), Aerodynamics for Engineering Students, Section 2.3.3, Butterworth-Heinemann, Oxford UK. ISBN 0-340-54847-9

References