Equioscillation theorem

The equioscillation theorem concerns the approximation of continuous functions using polynomials when the merit function is the maximum difference (uniform norm). Its discovery is attributed to Chebyshev.

Statement

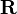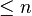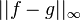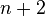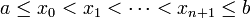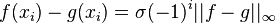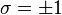Let $f$ be a continuous function from $[a,b]$ to $\mathbf{R}$ . Among all the polynomials of degree $\le n$ , the polynomial $g$ minimizes the uniform norm of the difference $|| f - g || _\infty$ if and only if there are $n+2$ points $a \le x_0 < x_1 < \cdots < x_{n+1} \le b$ such that $f(x_i) - g(x_i) = \sigma (-1)^i || f - g || _\infty$ where $\sigma = \pm 1$ .

Algorithms

Several minimax approximation algorithms are available, the most common being the Remez algorithm.

References

Notes on Notes on how to prove Chebyshev’s equioscillation theorem (Page no longer exists)
Another The Chebyshev Equioscillation Theorem by Robert Mayans (Misdirection)