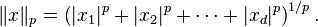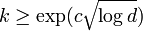Equilateral dimension

In mathematics, the equilateral dimension of a metric space is the maximum number of points that are all at equal distances from each other.^[1] Equilateral dimension has also been called "metric dimension", but the term "metric dimension" also has many other inequivalent usages.^[1] The equilateral dimension of a d-dimensional Euclidean space is d + 1, and the equilateral dimension of a d-dimensional vector space with the Chebyshev distance (L^∞ norm) is 2^d. However, the equilateral dimension of a space with the Manhattan distance (L¹ norm) is not known; Kusner's conjecture, named after Robert B. Kusner, states that it is exactly 2d.^[2]

Lebesgue spaces

The equilateral dimension has been particularly studied for Lebesgue spaces, finite-dimensional normed vector spaces with the L^p norm

\ \|x\|_p=\left(|x_1|^p+|x_2|^p+\cdots+|x_d|^p\right)^{1/p}.

The equilateral dimension of L^p spaces of dimension d behaves differently depending on the value of p:

For p = 1, the L^p norm gives rise to Manhattan distance. In this case, it is possible to find 2d equidistant points, the vertices of an axis-aligned cross polytope. The equilateral dimension is known to be exactly 2d for d ≤ 4,^[3] and to be upper bounded by O(d log d) for any d.^[4] Robert B. Kusner suggested in 1983 that the equilateral dimension for this case should be exactly 2d;^[5] this suggestion (together with a related suggestion for the equilateral dimension when p > 2) has come to be known as Kusner's conjecture.
For 1 < p < 2, the equilateral dimension is at least (1 + ε)d where ε is a constant that depends on p.^[6]
For p = 2, the L^p norm is the familiar Euclidean distance. The equilateral dimension of d-dimensional Euclidean space is d + 1: the d + 1 vertices of an equilateral triangle, regular tetrahedron, or higher-dimensional regular simplex form an equilateral set, and every equilateral set must have this form.^[5]
For 2 < p < ∞, the equilateral dimension is at least d + 1: for instance the d basis vectors of the vector space together with another vector of the form (−x, −x, ...) for a suitable choice of x form an equilateral set. Kusner's conjecture states that in these cases the equilateral dimension is exactly d + 1. Kusner's conjecture has been proven for the special case that p = 4.^[6] When p is an odd integer the equilateral dimension is upper bounded by O(d log d).^[4]
For p = ∞ (the limiting case of the L^p norm for finite values of p, in the limit as p grows to infinity) the L^p norm becomes the Chebyshev distance, the maximum absolute value of the differences of the coordinates. For a d-dimensional vector space with the Chebyshev distance, the equilateral dimension is 2^d: the 2^d vertices of an axis-aligned hypercube are at equal distances from each other, and no larger equilateral set is possible.^[5]

Normed vector spaces

Equilateral dimension has also been considered for normed vector spaces with norms other than the L^p norms. The problem of determining the equilateral dimension for a given norm is closely related to the kissing number problem: the kissing number in a normed space is the maximum number of disjoint translates of a unit ball that can all touch a single central ball, whereas the equilateral dimension is the maximum number of disjoint translates that can all touch each other.

For a normed vector space of dimension d, the equilateral dimension is at most 2^d; that is, the L^∞ norm has the highest equilateral dimension among all normed spaces.^[7] Petty (1971) asked whether every normed vector space of dimension d has equilateral dimension at least d + 1, but this remains unknown. There exist normed spaces in any dimension for which certain sets of four equilateral points cannot be extended to any larger equilateral set^[7] but these spaces may have larger equilateral sets that do not include these four points. For norms that are sufficiently close in Banach–Mazur distance to an L^p norm, Petty's question has a positive answer: the equilateral dimension is at least d + 1.^[8]

It is not possible for high-dimensional spaces to have bounded equilateral dimension: for any integer k, all normed vector spaces of sufficiently high dimension have equilateral dimension at least k.^[9] more specifically, according to a variation of Dvoretzky's theorem by Alon & Milman (1983), every d-dimensional normed space has a k-dimensional subspace that is close either to a Euclidean space or to a Chebyshev space, where

k\ge\exp(c\sqrt{\log d})

for some constant c. Because it is close to a Lebesgue space, this subspace and therefore also the whole space contains an equilateral set of at least k + 1 points. Therefore, the same superlogarithmic dependence on d holds for the lower bound on the equilateral dimension of d-dimensional space.^[8]

Riemannian manifolds

For any d-dimensional Riemannian manifold the equilateral dimension is at least d + 1.^[5] For a d-dimensional sphere, the equilateral dimension is d + 2, the same as for a Euclidean space of one higher dimension into which the sphere can be embedded.^[5] At the same time as he posed Kusner's conjecture, Kusner asked whether there exist Riemannian metrics with bounded dimension as a manifold but arbitrarily high equilateral dimension.^[5]

Notes

↑ 1.0 1.1 Deza & Deza (2009)
↑ Guy (1983); Koonen, Laurent & Schrijver (2000).
↑ Bandelt, Chepoi & Laurent (1998); Koonen, Laurent & Schrijver (2000).
↑ 4.0 4.1 Alon & Pudlák (2003).
↑ 5.0 5.1 5.2 5.3 5.4 5.5 Guy (1983).
↑ 6.0 6.1 Swanepoel (2004).
↑ 7.0 7.1 Petty (1971).
↑ 8.0 8.1 Swanepoel & Villa (2008).
↑ Braß (1999); Swanepoel & Villa (2008).

References

Alon, N.; Milman, V. D. (1983), "Embedding of $\scriptstyle l^{k}_{\infty}$ in finite-dimensional Banach spaces", Israel Journal of Mathematics 45 (4): 265–280, doi:10.1007/BF02804012, MR 720303 .
Alon, Noga; Pudlák, Pavel (2003), "Equilateral sets in l_pⁿ", Geometric and Functional Analysis 13 (3): 467–482, doi:10.1007/s00039-003-0418-7, MR 1995795 .
Bandelt, Hans-Jürgen; Chepoi, Victor; Laurent, Monique (1998), "Embedding into rectilinear spaces", Discrete and Computational Geometry 19 (4): 595–604, doi:10.1007/PL00009370, MR 1620076 .
Braß, Peter (1999), "On equilateral simplices in normed spaces", Contributions to Algebra and Geometry 40 (2): 303–307, MR 1720106 .
Deza, Michel Marie; Deza, Elena (2009), Encyclopedia of Distances, Springer-Verlag, p. 20 .
Guy, Richard K. (1983), "An olla-podrida of open problems, often oddly posed", American Mathematical Monthly 90 (3): 196–200, JSTOR 2975549, MR 1540158 .
Koolen, Jack; Laurent, Monique; Schrijver, Alexander (2000), "Equilateral dimension of the rectilinear space", Designs, Codes and Cryptography 21 (1): 149–164, doi:10.1023/A:1008391712305, MR 1801196 .
Petty, Clinton M. (1971), "Equilateral sets in Minkowski spaces", Proceedings of the American Mathematical Society 29 (2): 369–374, doi:10.1090/S0002-9939-1971-0275294-8, MR 0275294 .
Swanepoel, Konrad J. (2004), "A problem of Kusner on equilateral sets", Archiv der Mathematik 83 (2): 164–170, arXiv:math/0309317, doi:10.1007/s00013-003-4840-8, MR 2104945 .
Swanepoel, Konrad J.; Villa, Rafael (2008), "A lower bound for the equilateral number of normed spaces", Proceedings of the American Mathematical Society 136 (1): 127–131, arXiv:math/0603614, doi:10.1090/S0002-9939-07-08916-2, MR 2350397 .