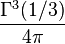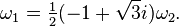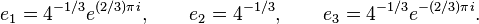Equianharmonic
In mathematics, and in particular the study of Weierstrass elliptic functions, the equianharmonic case occurs when the Weierstrass invariants satisfy g2 = 0 and g3 = 1. This page follows the terminology of Abramowitz and Stegun; see also the lemniscatic case. (These are special examples of complex multiplication.)
In the equianharmonic case, the minimal half period ω2 is real and equal to
where 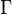 is the Gamma function. The half period is
is the Gamma function. The half period is
Here the period lattice is a real multiple of the Eisenstein integers.
The constants e1, e2 and e3 are given by
The case g2 = 0, g3 = a may be handled by a scaling transformation.