Equiangular lines

In geometry, a set of lines in Euclidean space is called equiangular if every pair of lines makes the same angle.

Computing the maximum number of equiangular lines in n-dimensional Euclidean space is a difficult problem, and unsolved in general, though bounds are known. The maximal number of equiangular lines in 2-dimensional Euclidean space is 3: we can take the lines through opposite vertices of a regular hexagon, each at an angle 120 degrees from the other two. The maximum in 3 dimensions is 6: we can take lines through opposite vertices of an icosahedron. The maximum in dimensions 1 through 18 is listed in The On-Line Encyclopedia of Integer Sequences as follows:

1, 3, 6, 6, 10, 16, 28, 28, 28, 28, 28, 28, 28, 28, 36, 40, 48, 48, ...

In particular, the maximum number of equiangular lines in 7 dimensions is 28. We can obtain these lines as follows. Take the vector (-3,-3,1,1,1,1,1,1) in 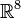$\mathbb{R}^8$ , and form all 28 vectors obtained by permuting the components of this. The dot product of two of these vectors is 8 if both have a component 3 in the same place or -8 otherwise. Thus, the lines through the origin containing these vectors are equiangular. Moreoever, all 28 vectors are orthogonal to the vector (1,1,1,1,1,1,1,1) in 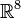$\mathbb{R}^8$ , so they lie in a 7-dimensional space. In fact, these 28 vectors and their negatives are, up to rotation and dilation, the 56 vertices of the 3₂₁ polytope. In other words, they are the weight vectors of the 56-dimensional representation of the Lie group E₇.

Equiangular lines are equivalent to two-graphs. Given a set of equiangular lines, let c be the cosine of the common angle. We assume that the angle is not 90°, since that case is trivial (i.e., not interesting, because the lines are just coordinate axes); thus, c is nonzero. We may move the lines so they all pass through the origin of coordinates. Choose one unit vector in each line. Form the matrix M of inner products. This matrix has 1 on the diagonal and ±c everywhere else, and it is symmetric. Subtracting the identity matrix I and dividing by c, we have a symmetric matrix with zero diagonal and ±1 off the diagonal. This is the Seidel adjacency matrix of a two-graph. Conversely, every two-graph can be represented as a set of equiangular lines.^[1]

Notes

↑ van Lint & Seidel 1966

References

The On-Line Encyclopedia of Integer Sequences, Maximal size of a set of equiangular lines in n dimensions, sequence number A002853.
Brouwer, A.E., Cohen, A.M., and Neumaier, A. Distance-Regular Graphs. Springer-Verlag, Berlin, 1989. Section 3.8.
Godsil, Chris; Royle, Gordon (2001), Algebraic Graph Theory, Graduate Texts in Mathematics 207, New York: Springer-Verlag . (See Chapter 11.)
Gosselin, S., Regular two-graphs and equiangular lines, Master's thesis, Mathematics Department, University of Waterloo, 2004.
van Lint, J. H.; Seidel, J. J. (1966), "Equilateral point sets in elliptic geometry", Indagationes Mathematicae, Proc. Koninkl. Ned. Akad. Wetenschap. Ser. A 69 28: 335–348