Enneagonal antiprism
| Uniform Enneagonal antiprism | |
|---|---|
 | |
| Type | Prismatic uniform polyhedron |
| Elements | F = 20, E = 36 V = 18 (χ = 2) |
| Faces by sides | 18{3}+2{9} |
| Schläfli symbol | s{2,18} sr{2,9} |
| Wythoff symbol | | 2 2 9 |
| Coxeter-Dynkin | |
| Symmetry group | D9d, [2+,18], (2*9), order 36 |
| Rotation group | D9, [9,2]+, (922), order 18 |
| References | U77(g) |
| Dual | Enneagonal trapezohedron |
| Properties | convex |
 Vertex figure 3.3.3.9 | |
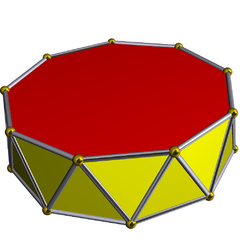
In geometry, the enneagonal antiprism is one in an infinite set of convex antiprisms formed by triangle sides and two regular polygon caps, in this case two enneagons.
If faces are all regular, it is a semiregular polyhedron.
See also
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | n |
|---|---|---|---|---|---|---|---|---|---|---|---|
| s{2,4} sr{2,2} |
s{2,6} sr{2,3} |
s{2,8} sr{2,4} |
s{2,10} sr{2,5} |
s{2,12} sr{2,6} |
s{2,14} sr{2,7} |
s{2,16} sr{2,8} |
s{2,18} sr{2,9} |
s{2,20} sr{2,10} |
s{2,22} sr{2,11} |
s{2,24} sr{2,12} |
s{2,2n} sr{2,n} |
| As spherical polyhedra | |||||||||||
External links
- Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra
- VRML model
- Conway Notation for Polyhedra Try: "A9"