Elementary matrix

In mathematics, an elementary matrix is a matrix which differs from the identity matrix by one single elementary row operation. The elementary matrices generate the general linear group of invertible matrices. Left multiplication (pre-multiplication) by an elementary matrix represents elementary row operations, while right multiplication (post-multiplication) represents elementary column operations. The acronym "ERO" is commonly used for "elementary row operations".

Elementary row operations are used in Gaussian elimination to reduce a matrix to row echelon form. They are also used in Gauss-Jordan elimination to further reduce the matrix to reduced row echelon form.

Operations

There are three types of elementary matrices, which correspond to three types of row operations (respectively, column operations):

Row switching
A row within the matrix can be switched with another row.
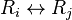
R_i \leftrightarrow R_j
Row multiplication
Each element in a row can be multiplied by a non-zero constant.
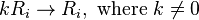
kR_i \rightarrow R_i,\ \mbox{where } k \neq 0
Row addition
A row can be replaced by the sum of that row and a multiple of another row.
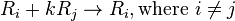
R_i + kR_j \rightarrow R_i, \mbox{where } i \neq j

If E is an elementary matrix, as described below, to apply the elementary row operation to a matrix A, one multiplies the elementary matrix on the left, E⋅A. The elementary matrix for any row operation is obtained by executing the operation on the identity matrix.

Row-switching transformations

The first type of row operation on a matrix A switches all matrix elements on row i with their counterparts on row j. The corresponding elementary matrix is obtained by swapping row i and row j of the identity matrix.

T_{i,j} = \begin{bmatrix} 1 & & & & & & & \\ & \ddots & & & & & & \\ & & 0 & & 1 & & \\ & & & \ddots & & & & \\ & & 1 & & 0 & & \\ & & & & & & \ddots & \\ & & & & & & & 1\end{bmatrix}\quad
So Tij⋅A is the matrix produced by exchanging row i and row j of A.

Properties

  • The inverse of this matrix is itself: Tij−1=Tij.
  • Since the determinant of the identity matrix is unity, det[Tij] = −1. It follows that for any square matrix A (of the correct size), we have det[TijA] = −det[A].

Row-multiplying transformations

The next type of row operation on a matrix A multiplies all elements on row i by m where m is a non-zero scalar (usually a real number). The corresponding elementary matrix is a diagonal matrix, with diagonal entries 1 everywhere except in the ith position, where it is m.

T_i(m) = \begin{bmatrix} 1 & & & & & & \\ & \ddots & & & & & \\ & & 1 & & & & \\ & & & m & & & \\ & & & & 1 & & \\ & & & & & \ddots & \\ & & & & & & 1\end{bmatrix}\quad
So Ti(m)⋅A is the matrix produced from A by multiplying row i by m.

Properties

  • The inverse of this matrix is: Ti(m)−1 = Ti(1/m).
  • The matrix and its inverse are diagonal matrices.
  • det[Ti(m)] = m. Therefore for a square matrix A (of the correct size), we have det[Ti(m)A] = m det[A].

Row-addition transformations

The final type of row operation on a matrix A adds row j multiplied by a scalar m to row i. The corresponding elementary matrix is the identity matrix but with an m in the (i,j) position.

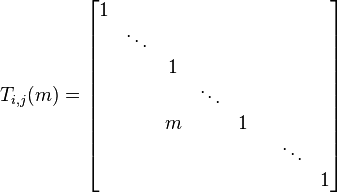
T_{i,j}(m) = \begin{bmatrix} 1 & & & & & & & \\ & \ddots & & & & & & \\ & & 1 & & & & & \\ & & & \ddots & & & & \\ & & m & & 1 & & \\ & & & & & & \ddots & \\ & & & & & & & 1\end{bmatrix}
So Ti,j(m)⋅A is the matrix produced from A by adding m times row j to row i.

Properties

  • These transformations are a kind of shear mapping, also known as a transvections.
  • Tij(m)−1 = Tij(−m) (inverse matrix).
  • The matrix and its inverse are triangular matrices.
  • det[Tij(m)] = 1. Therefore, for a square matrix A (of the correct size) we have det[Tij(m)A] = det[A].
  • Row-addition transforms satisfy the Steinberg relations.

See also

References