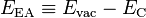Electron affinity

In chemistry and atomic physics, the electron affinity of an atom or molecule is defined as the amount of energy released when an electron is added to a neutral atom or molecule in the gaseous state to form a negative ion.^[1]

X + e⁻ → X⁻ + energy

In solid state physics, the electron affinity for a surface is defined somewhat differently (see below).

Measurement and use of electron affinity

This property is measured for atoms and molecules in the gaseous state only, since in a solid or liquid states their energy levels would be changed by contact with other atoms or molecules. A list of the electron affinities was used by Robert S. Mulliken to develop an electronegativity scale for atoms, equal to the average of the electron affinity and ionization potential.^[2][3] Other theoretical concepts that use electron affinity include electronic chemical potential and chemical hardness. Another example, a molecule or atom that has a more positive value of electron affinity than another is often called an electron acceptor and the less positive an electron donor. Together they may undergo charge-transfer reactions.

Sign convention

To use electron affinities properly, it is essential to keep track of sign. For any reaction that releases energy, the change ΔE in total energy has a negative value and the reaction is called an exothermic process. Electron capture for almost all non-noble gas atoms involves the release of energy^[4] and thus are exothermic. The positive values that are listed in tables of E_ea are amounts or magnitudes. It is the word, released within the definition energy released that supplies the negative sign to ΔE. Confusion arises in mistaking E_ea for a change in energy, ΔE, in which case the positive values listed in tables would be for an endo- not exo-thermic process. The relation between the two is E_ea = −ΔE(attach).

However, if the value assigned to E_ea is negative, the negative sign implies a reversal of direction, and energy is required to attach an electron. In this case, the electron capture is an endothermic process and the relationship, E_ea = −ΔE(attach) is still valid. Negative values typically arise for the capture of a second electron, but also for the nitrogen atom.

The usual expression for calculating E_ea when an electron is attached is

E_ea = (E_initial − E_final)_attach = −ΔE(attach)

This expression does follow the convention ΔX = X(final) − X(initial) since −ΔE = −(E(final) − E(initial)) = E(initial) − E(final).

Equivalently, electron affinity can also be defined as the amount of energy required to detach an electron from a singly charged negative ion,^[1] i.e. the energy change for the process

X⁻ → X + e⁻

If the same table is employed for the forward and reverse reactions, without switching signs, care must be taken to apply the correct definition to the corresponding direction, attachment (release) or detachment (require). Since almost all detachments (require +) an amount of energy listed on the table, those detachment reactions are endothermic, or ΔE(detach) > 0.

Electron affinities of the elements

EA vs Atomic Number

Although E_ea varies greatly across the periodic table, some patterns emerge. Generally, nonmetals have more positive E_ea than metals. Atoms whose anions are more stable than neutral atoms have a greater E_ea. Chlorine most strongly attracts extra electrons; mercury most weakly attracts an extra electron. The electron affinities of the noble gases have not been conclusively measured, so they may or may not have slightly negative values.

E_ea generally increases across a period (row) in the periodic table. This is caused by the filling of the valence shell of the atom; a Group 17 atom releases more energy than a Group 1 atom on gaining an electron because it obtains a filled valence shell and therefore is more stable.

A trend of decreasing E_ea going down the groups in the periodic table might be expected. The additional electron will be entering an orbital farther away from the nucleus. Since this electron is farther from the nucleus it is less attracted to the nucleus and would release less energy when added. However, a clear counterexample to this trend can be found in Group 2, and inspecting the entire periodic table, it turns out that the proposed trend only applies to Group 1 atoms.

Thus, electron affinity follows the left-right trend of electronegativity but not the up-down trend.

The following data are quoted in kJ/mol. Elements marked with an asterisk are expected to have electron affinities close to zero on quantum mechanical grounds.

Electron affinities in the periodic table
Group →	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
↓ Period
1	H 73																	He *
2	Li 60	Be *											B 27	C 122	N *	O 141	F 328	Ne *
3	Na 53	Mg *											Al 42	Si 134	P 72	S 200	Cl 349	Ar *
4	K 48	Ca 2	Sc 18	Ti 8	V 51	Cr 65	Mn *	Fe 15	Co 64	Ni 112	Cu 119	Zn *	Ga 41	Ge 119	As 79	Se 195	Br 324	Kr *
5	Rb 47	Sr 5	Y 30	Zr 41	Nb 86	Mo 72	Tc *	Ru 101	Rh 110	Pd 54	Ag 126	Cd *	In 39	Sn 107	Sb 101	Te 190	I 295	Xe *
6	Cs 46	Ba 14		Hf	Ta 31	W 79	Re *	Os 104	Ir 150	Pt 205	Au 223	Hg *	Tl 36	Pb 35	Bi 91	Po	At	Rn *
7	Fr	Ra		Rf	Db	Sg	Bh	Hs	Mt	Ds	Rg	Cn	Uut	Fl	Uup	Lv	Uus	Uuo
			La 45	Ce 92	Pr	Nd	Pm	Sm	Eu	Gd	Tb	Dy	Ho	Er	Tm 99	Yb	Lu 33
			Ac	Th	Pa	U	Np	Pu	Am	Cm	Bk	Cf	Es	Fm	Md	No	Lr
Legend
The number mentioned is Electron affinity in kJ/mol (rounded)
For the equivalent value in eV, see: Electron affinity (data page)
* Denotes elements that are expected to have electron affinities close to zero on quantum mechanical grounds
Primordial From decay Synthetic Border shows natural occurrence of the element Background color shows subcategory in the metal–metalloid–nonmetal trend: Metal Metalloid Nonmetal Unknown chemical properties Alkali metal Alkaline earth metal Lan­thanide Actinide Transition metal Post-​transition metal Polyatomic nonmetal Diatomic nonmetal Noble gas

Molecular electron affinities

The electron affinity of molecules is a complicated function of their electronic structure. For instance the electron affinity for benzene is negative, as is that of naphthalene, while those of anthracene, phenanthrene and pyrene are positive. In silico experiments show that the electron affinity of hexacyanobenzene surpasses that of fullerene.^[5]

"Electron affinity" as defined in solid state physics

Band diagram of semiconductor-vacuum interface showing electron affinity E_EA, defined as the difference between near-surface vacuum energy E_vac, and near-surface conduction band edge E_C. Also shown: Fermi level E_F, valence band edge E_V, work function W.

In the field of solid state physics, the electron affinity is defined differently than in chemistry and atomic physics, not only in that it applies to a different system, but also because it is temperature dependent. For a semiconductor-vacuum interface (that is, the surface of a semiconductor), electron affinity, typically denoted by E_EA or χ, is defined as the energy obtained by moving an electron from the vacuum just outside the semiconductor to the bottom of the conduction band just inside the semiconductor:^[6]

In an intrinsic semiconductor at absolute zero, this concept is functionally analogous to the chemistry definition of electron affinity, since an added electron will spontaneously go to the bottom of the conduction band. At nonzero temperature, and for other materials (metals, semimetals, heavily doped semiconductors), the analogy does not hold since an added electron will instead go to the Fermi level on average. In any case, the value of the electron affinity of a solid substance is very different from the chemistry and atomic physics electron affinity value for an atom of the same substance in gas phase. For example, a silicon crystal surface has electron affinity 4.05 eV, whereas an isolated silicon atom has electron affinity 1.39 eV.

The electron affinity can be contrasted with the work function. The work function is the thermodynamic work that can be obtained by reversibly, isothermally moving an electron from the vacuum to the material; this thermodynamic electron goes to the Fermi level on average, not the conduction band edge: 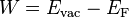. While the work function of a semiconductor can be changed by doping, the electron affinity ideally does not change with doping and so it is closer to being a material constant. However, the electron affinity does depend on the surface termination (crystal face, surface chemistry, etc.).

In certain circumstances, the electron affinity may become negative.^[7] Often negative electron affinity is desired to obtain efficient cathodes that can supply electrons to the vacuum with little energy loss. The observed electron yield as a function of various parameters such as bias voltage or illumination conditions can be used to describe these structures with band diagrams in which the electron affinity is one parameter. For one illustration of the apparent effect of surface termination on electron emission, see Figure 3 in Marchywka Effect.

In semiconductor physics, the primary use of the electron affinity is not actually in the analysis of semiconductor-vacuum junctions, but rather in heuristic electron affinity rules for estimating the band bending that occurs at the interface of two materials.

See also

• Ionization energy — a closely related concept describing the energy required to remove an electron from a neutral atom or molecule
• One-electron reduction
• Electron-capture mass spectrometry
• Electronegativity
• Valence electron
• Vacuum level
• Electron donor

References

• Tro, Nivaldo J. (2008). Chemistry: A Molecular Approach (2nd Edn.). New Jersey: Pearson Prentice Hall. ISBN 0-13-100065-9. pp. 348–349.

External links

• Electron affinity, definition from the IUPAC Gold Book