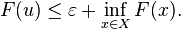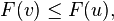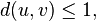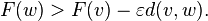Ekeland's variational principle

In mathematical analysis, Ekeland's variational principle, discovered by Ivar Ekeland,[1][2][3] is a theorem that asserts that there exists nearly optimal solutions to some optimization problems.

Ekeland's variational principle can be used when the lower level set of a minimization problems is not compact, so that the Bolzano–Weierstrass theorem can not be applied. Ekeland's principle relies on the completeness of the metric space.[4]

Ekeland's principle leads to a quick proof of the Caristi fixed point theorem.[4][5]

Ekeland's principle has been shown by F. Sullivan to be equivalent to completeness of metric spaces.

Ekeland was associated with the Paris Dauphine University when he proposed this theorem.[1]

Statement of the theorem

Let (X, d) be a complete metric space, and let F: X → R ∪ {+∞} be a lower semicontinuous functional on X that is bounded below and not identically equal to +∞. Fix ε > 0 and a point u ∈ X such that

F(u) \leq \varepsilon + \inf_{x \in X} F(x).

Then there exists a point v ∈ X such that

F(v) \leq F(u),
d(u, v) \leq 1,

and, for all w ≠ v,

F(w) > F(v) - \varepsilon d(v, w).

This theorem has been shown by F. Sullivan to be equivalent to completeness for metric spaces.

References

  1. ↑ 1.0 1.1 Ekeland, Ivar (1974). "On the variational principle". J. Math. Anal. Appl. 47: 324–353. doi:10.1016/0022-247X(74)90025-0. ISSN 0022-247X.
  2. ↑ Ekeland, Ivar (1979). "Nonconvex minimization problems". Bulletin of the American Mathematical Society. New Series 1 (3): 443–474. doi:10.1090/S0273-0979-1979-14595-6. MR 526967.
  3. ↑ Ekeland, Ivar; Temam, Roger (1999). Convex analysis and variational problems. Classics in applied mathematics 28 (Corrected reprinting of the (1976) North-Holland ed.). Philadelphia, PA: Society for Industrial and Applied Mathematics (SIAM). pp. 357–373. ISBN 0-89871-450-8. MR 1727362.
  4. ↑ 4.0 4.1 Kirk, William A.; Goebel, Kazimierz (1990). Topics in Metric Fixed Point Theory. Cambridge University Press. ISBN 0-521-38289-0.
  5. ↑ Ok, Efe (2007). "D: Continuity I". Real Analysis with Economic Applications. Princeton University Press. p. 664. ISBN 978-0-691-11768-3. Retrieved January 31, 2009.

Further reading