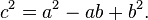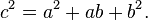Eisenstein triple

Similar to a Pythagorean triple, an Eisenstein triple is a set of integers which are the lengths of the sides of a triangle where one of the angles is 60 degrees.

Triangles with an angle of 60°

An Eisenstein triple

Triangles with an angle of 60° are a special case of the Law of Cosines:[1][2][3]

c^2 = a^2 - ab + b^2.

When the lengths of the sides are integers, the values form a set known as an Eisenstein triple.[4]

Examples of Eisenstein triples include:[5]

Side a Side b Side c
3 8 7
5 8 7
5 21 19
7 40 37

Triangles with an angle of 120°

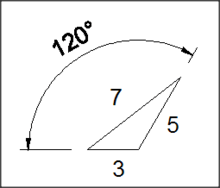
Triangle with 120° angle and integer sides

A similar special case of the Law of Cosines relates the sides of a triangle with an angle of 120 degrees:

c^2 = a^2 + ab + b^2.

Examples of such triangles include:[6]

Side a Side b Side c
3 5 7
7 8 13
5 16 19

See also

References

  1. ↑ Gilder, J., Integer-sided triangles with an angle of 60°," Mathematical Gazette 66, December 1982, 261 266
  2. ↑ Burn, Bob, "Triangles with a 60° angle and sides of integer length," Mathematical Gazette 87, March 2003, 148–153.
  3. ↑ Read, Emrys, "On integer-sided triangles containing angles of 120° or 60°", Mathematical Gazette, 90, July 2006, 299–305.
  4. ↑ http://www2.edc.org/cme/showcase/slides.delaware.2006.pdf
  5. ↑ http://www.had2know.com/academics/integer-triangles-60-degree-angle.html
  6. ↑ http://www.had2know.com/academics/integer-triangles-120-degree-angle.html

External links