Eilenberg–Ganea theorem
In mathematics, particularly in homological algebra and algebraic topology, the Eilenberg–Ganea theorem states for every finitely generated group G with certain conditions on its cohomological dimension (namely 3 ≤ cd(G) ≤ n), one can construct an aspherical CW complex X of dimension n whose fundamental group is G. The theorem is named after Polish mathematician Samuel Eilenberg and Romanian mathematician Tudor Ganea. The theorem was first published in a short paper in 1957 in the Annals of Mathematics.[1]
Definitions
Group cohomology: Let G be a group and X = K(G, 1) is the corresponding Eilenberg−MacLane space. Then we have the following singular chain complex which is a free resolution of Z over the group ring Z[G] (where Z is a trivial Z[G] module).
where E is the universal cover of X and Ck(E) is the free abelian group generated by singular k chains. Group cohomology of the group G with coefficient in G module M is the cohomology of this chain complex with coefficient in M and is denoted by H*(G, M).
Cohomological dimension: G has cohomological dimension n with coefficients in Z (denoted by cdZ(G)) if
Fact: If G has a projective resolution of length ≤ n, i.e. Z as trivial Z[G] module has a projective resolution of length ≤ n if and only if HiZ(G,M) = 0 for all Z module M and for all i > n.
Therefore we have an alternative definition of cohomological dimension as follows,
Cohomological dimension of G with coefficient in Z is the smallest n (possibly infinity) such that G has a projective resolution of length n, i.e. Z has a projective resolution of length n as a trivial Z[G] module.
Eilenberg−Ganea theorem
Let G be a finitely presented group and n ≥ 3 be an integer. Suppose cohomological dimension of G with coefficients in Z, i.e. cdZ(G) ≤ n. Then there exists an n-dimensional aspherical CW complex X such that the fundamental group of X is G i.e. π1(X) = G.
Converse
Converse of this theorem is an consequence of cellular homology, and the fact that every free module is projective.
Theorem: Let X be an aspherical n-dimensional CW complex with π1(X) = G, then cdZ(G) ≤ n.
Related results and conjectures
For n = 1 the result is one of the consequences of Stallings theorem about ends of groups.[2]
Theorem: Every finitely generated group of cohomological dimension one is free.
For n = 2 the statement is known as Eilenberg–Ganea conjecture.
Eilenberg−Ganea Conjecture: If a group G has cohomological dimension 2 then there is a 2-dimensional aspherical CW complex X with π1(X) = G.
It is known that given a group G with cdZ(G) = 2 there exists a 3-dimensional aspherical CW complex X with π1(X) = G.
See also
- Eilenberg−Ganea conjecture
- Group cohomology
- Cohomological dimension
- Stallings theorem about ends of groups
References
- ↑
- Eilenberg, Samuel; Ganea, Tudor (1957). "On the Lusternik–Schnirelmann category of abstract groups". Annals of Mathematics. 2nd Ser. 65 (3): 517–518. doi:10.2307/1970062. MR 0085510.
- ↑
- John R. Stallings, "On torsion-free groups with infinitely many ends", Annals of Mathematics 88 (1968), 312–334. MR 0228573
- Bestvina, Mladen; Brady, Noel (1997). "Morse theory and finiteness properties of groups". Inventiones Mathematicae 129 (3): 445–470. doi:10.1007/s002220050168. MR 1465330..
- Kenneth S. Brown, Cohomology of groups, Corrected reprint of the 1982 original, Graduate Texts in Mathematics, 87, Springer-Verlag, New York, 1994. MR 1324339. ISBN 0-387-90688-6
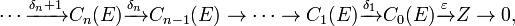
![n=\sup \{k : \text{There exists a }Z[G]\text{ module }M\text{ with }H^{k}(G,M)\neq 0\}.](../I/m/0359246a8990d75c158b1796a61aa445.png)