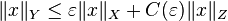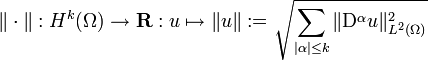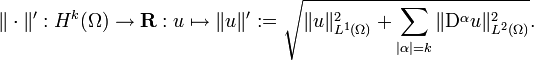Ehrling's lemma

In mathematics, Ehrling's lemma is a result concerning Banach spaces. It is often used in functional analysis to demonstrate the equivalence of certain norms on Sobolev spaces. It was proposed by Gunnar Ehrling.

Statement of the lemma

Let (X, ||·||_X), (Y, ||·||_Y) and (Z, ||·||_Z) be three Banach spaces. Assume that:

X is compactly embedded in Y: i.e. X ⊆ Y and every ||·||_X-bounded sequence in X has a subsequence that is ||·||_Y-convergent; and
Y is continuously embedded in Z: i.e. Y ⊆ Z and there is a constant k so that ||y||_Z ≤ k||y||_Y for every y ∈ Y.

Then, for every ε > 0, there exists a constant C(ε) such that, for all x ∈ X,

\| x \|_{Y} \leq \varepsilon \| x \|_{X} + C(\varepsilon) \| x \|_{Z}

Corollary (equivalent norms for Sobolev spaces)

Let Ω ⊂ Rⁿ be open and bounded, and let k ∈ N. Suppose that the Sobolev space H^k(Ω) is compactly embedded in H^k−1(Ω). Then the following two norms on H^k(Ω) are equivalent:

\| \cdot \| : H^{k} (\Omega) \to \mathbf{R}: u \mapsto \| u \| := \sqrt{\sum_{| \alpha | \leq k} \| \mathrm{D}^{\alpha} u \|_{L^{2} (\Omega)}^{2}}

and

\| \cdot \|' : H^{k} (\Omega) \to \mathbf{R}: u \mapsto \| u \|' := \sqrt{\| u \|_{L^{1} (\Omega)}^{2} + \sum_{| \alpha | = k} \| \mathrm{D}^{\alpha} u \|_{L^{2} (\Omega)}^{2}}.

For the subspace of H^k(Ω) consisting of those Sobolev functions with zero trace (those that are "zero on the boundary" of Ω), the L¹ norm of u can be left out to yield another equivalent norm.

References

Renardy, Michael; Rogers, Robert C. (1992). An Introduction to Partial Differential Equations. Berlin: Springer-Verlag. ISBN 978-3-540-97952-4.