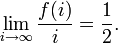Ehrenfeucht–Mycielski sequence
The Ehrenfeucht–Mycielski sequence is a recursively defined sequence of binary digits with pseudorandom properties, defined by Andrzej Ehrenfeucht and Jan Mycielski (1992).
Definition
The sequence starts with the single bit 0; each successive digit is formed by finding the longest suffix of the sequence that also occurs earlier within the sequence, and complementing the bit following the most recent earlier occurrence of that suffix. (The empty string is a suffix and prefix of every string.) For example, the first few steps of this construction process are:
- 0: initial bit
- 01: the suffix "" of "0" occurs earlier, most-recently followed by a 0, so add 1
- 010: the suffix "" of "01" occurs earlier, most-recently followed by a 1, so add 0
- 0100: the suffix "0" of "010" occurs earlier, most-recently followed by a 1, so add 0
- 01001: the suffix "0" of "0100" occurs earlier, most-recently followed by a 0, so add 1
- 010011: the suffix "01" of "01001" occurs earlier, most-recently followed by a 0, so add 1
- 0100110: the suffix "1" of "010011" occurs earlier, most-recently followed by a 1, so add 0
The first few digits of the sequence are:
Algorithms
A naive algorithm that generates each bit in the sequence by comparing each suffix with the entire previous sequence could take as much as O(n3) time to generate the first n bits of the sequence; however, as Herman & Soltys (2009) show using a data structure related to a suffix tree, the sequence can be generated much more efficiently, in constant time per generated digit.
Universality
The sequence is disjunctive; i.e., every finite subsequence of bits occurs contiguously, infinitely often within the sequence (Ehrenfeucht & Mycielski 1992). More explicitly, the position by which every subsequence of length i can be guaranteed to have occurred at least j times is at most A(4i,j), where A is the Ackermann function (Herman & Soltys 2009). Experimentally, however, each subsequence appears much earlier in this sequence than this upper bound would suggest: the position by which all length-i sequences occur, up to the limit of experimental testing, is close to the minimum possible value it could be, 2i + i, the position by which a de Bruijn sequence contains all length-i substrings (Sutner 2003).
Normality
Ehrenfeucht & Mycielski (1992) conjecture that the numbers of 0 and 1 bits each converge to a limiting density of 1/2. That is, if f(i) denotes the number of 0 bits in the first i positions of the Ehrenfeucht–Mycielski sequence, then it should be the case that
More strongly, I. J. Good suggests that the convergence rate of this limit should be significantly faster than that of a random binary sequence, for which (by the law of the iterated logarithm) 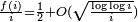 (Ehrenfeucht & Mycielski 1992).
The Ehrenfeucht–Mycielski balance conjecture suggests that the binary number 0.01001101... (the number having the Ehrenfeucht–Mycielski sequence as its sequence of binary digits after the binary point) may be a normal number in base 2.
As of 2009 this conjecture remains unproven (Herman & Soltys 2009); however, it is known that every limit point of the sequence of values f(i)/i lies within the interval [1/4,3/4] (Kieffer & Szpankowski 2007).
(Ehrenfeucht & Mycielski 1992).
The Ehrenfeucht–Mycielski balance conjecture suggests that the binary number 0.01001101... (the number having the Ehrenfeucht–Mycielski sequence as its sequence of binary digits after the binary point) may be a normal number in base 2.
As of 2009 this conjecture remains unproven (Herman & Soltys 2009); however, it is known that every limit point of the sequence of values f(i)/i lies within the interval [1/4,3/4] (Kieffer & Szpankowski 2007).
References
- Ehrenfeucht, Andrzej; Mycielski, Jan (1992), Guy, Richard K., ed., "Unsolved problems", American Mathematical Monthly 99: 373–375, JSTOR 2324917
|chapter=ignored (help). - Herman, Grzegorz; Soltys, Michael (2009), "On the Ehrenfeucht–Mycielski sequence", Journal of Discrete Algorithms 7 (4): 500–508, doi:10.1016/j.jda.2009.01.002.
- Kieffer, John C.; Szpankowski, Wojciech (2007), "On the Ehrenfeucht–Mycielski balance conjecture", Proc. Conf. Analysis of Algorithms (AofA 2007), Discrete Mathematics and Theoretical Computer Science, pp. 19–28.
- Sutner, Klaus (2003), "The Ehrenfeucht–Mycielski sequence", in Ibarra, O. H.; Dang, Z., Proc. Conf. Implementation and Application of Automata (CIAA 2003), Lecture Notes in Computer Science 2759, Springer-Verlag, pp. 73–82, doi:10.1007/3-540-45089-0_26.
External links
- One million terms of the sequence calculated by Terry McConnell at Syracuse University.