Ehrenfeucht–Fraïssé game

In the mathematical discipline of model theory, the Ehrenfeucht–Fraïssé game (also called back-and-forth games) is a technique for determining whether two structures are elementarily equivalent. The main application of Ehrenfeucht–Fraïssé games is in proving the inexpressibility of certain properties in first-order logic. Indeed, Ehrenfeucht–Fraïssé games provide a complete methodology for proving inexpressibility results for first-order logic. In this role, these games are of particular importance in finite model theory and its applications in computer science (specifically Computer Aided Verification and database theory), since Ehrenfeucht–Fraïssé games are one of the such few techniques from model theory that remain valid in the context of finite models. Other widely used techniques for proving inexpressibility results, such as the compactness theorem, do not work in finite models.

Ehrenfeucht–Fraïssé like games can also be defined for other logics, such as fixpoint logics^[1] and pebble games for finite variable logics; extensions are powerful enough to characterise definability in existential second-order logic.

Main idea

The main idea behind the game is that we have two structures, and two players (defined below). One of the players wants to show that the two structures are different, whereas the other player wants to show that they are somewhat similar (according to first-order logic). The game is played in turns and rounds; A round proceeds as follows: First the first player (Spoiler) chooses any element from one of the structures, and the other player chooses an element from the other structure. The other player's task is to always pick an element that is "similar" to the one that Spoiler chose. The second player (Duplicator) wins if there exists an isomorphism between the elements chosen in the two different structures.

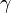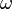The game lasts for a fixed amount of steps ( $\gamma$ ) (an ordinal, but usually a finite number or $\omega$ ).

Definition

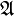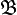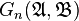Suppose that we are given two structures $\mathfrak{A}$ and $\mathfrak{B}$ , each with no function symbols and the same set of relation symbols, and a fixed natural number n. We can then define the Ehrenfeucht–Fraïssé game $G_n(\mathfrak{A},\mathfrak{B})$ to be a game between two players, Spoiler and Duplicator, played as follows:

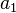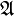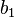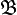The first player, Spoiler, picks either a member $a_1$ of $\mathfrak{A}$ or a member $b_1$ of $\mathfrak{B}$ .
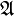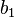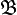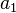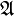If Spoiler picked a member of $\mathfrak{A}$ , Duplicator picks a member $b_1$ of $\mathfrak{B}$ ; otherwise, Duplicator picks a member $a_1$ of $\mathfrak{A}$ .
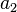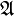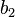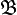Spoiler picks either a member $a_2$ of $\mathfrak{A}$ or a member $b_2$ of $\mathfrak{B}$ .
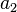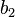Duplicator picks an element $a_2$ or $b_2$ in the model from which Spoiler did not pick.
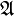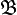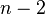Spoiler and Duplicator continue to pick members of $\mathfrak{A}$ and $\mathfrak{B}$ for $n-2$ more steps.
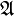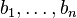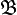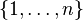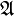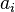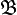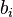At the conclusion of the game, we have chosen distinct elements $a_1, \dots, a_n$ of $\mathfrak{A}$ and $b_1, \dots, b_n$ of $\mathfrak{B}$ . We therefore have two structures on the set $\{1, \dots,n\}$ , one induced from $\mathfrak{A}$ via the map sending $i$ to $a_i$ , and the other induced from $\mathfrak{B}$ via the map sending $i$ to $b_i$ . Duplicator wins if these structures are the same; Spoiler wins if they are not.

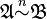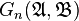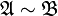For each n we define a relation $\mathfrak{A} \stackrel{n}{\sim} \mathfrak{B}$ if Duplicator wins the n-move game $G_n(\mathfrak{A},\mathfrak{B})$ . These are all equivalence relations on the class of structures with the given relation symbols. The intersection of all these relations is again an equivalence relation $\mathfrak{A} \sim \mathfrak{B}$ .

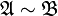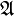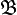It is easy to prove that if Duplicator wins this game for all n, that is, $\mathfrak{A} \sim \mathfrak{B}$ , then $\mathfrak{A}$ and $\mathfrak{B}$ are elementarily equivalent. If the set of relation symbols being considered is finite, the converse is also true.

History

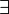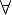The back-and-forth method used in the Ehrenfeucht–Fraïssé game to verify elementary equivalence was given by Roland Fraïssé in his thesis;^[2]^[3] it was formulated as a game by Andrzej Ehrenfeucht.^[4] The names Spoiler and Duplicator are due to Joel Spencer.^[5] Other usual names are Eloise [sic] and Abelard (and often denoted by $\exists$ and $\forall$ ) after Heloise and Abelard, a naming scheme introduced by Wilfrid Hodges in his book Model Theory.

References

↑ Bosse, Uwe (1993). "An Ehrenfeucht–Fraïssé game for fixpoint logic and stratified fixpoint logic". In last=Börger, Egon. Computer Science Logic: 6th Workshop, CSL'92, San Miniato, Italy, September 28 - October 2, 1992. Selected Papers. Lecture Notes in Computer Science 702. Springer-Verlag. pp. 100–114. ISBN 3-540-56992-8. Zbl 0808.03024.
↑ Sur une nouvelle classification des systèmes de relations, Roland Fraïssé, Comptes Rendus 230 (1950), 1022–1024.
↑ Sur quelques classifications des systèmes de relations, Roland Fraïssé, thesis, Paris, 1953; published in Publications Scientifiques de l'Université d'Alger, series A 1 (1954), 35–182.
↑ An application of games to the completeness problem for formalized theories, A. Ehrenfeucht, Fundamenta Mathematicae 49 (1961), 129–141.
↑ Stanford Encyclopedia of Philosophy, entry on Logic and Games.
↑ A Course in Model Theory, Bruno Poizat, tr. Moses Klein, New York: Springer-Verlag, 2000.
↑ Linear Orderings, Joseph G. Rosenstein, New York: Academic Press, 1982.
↑ Example of the Ehrenfeucht-Fraïssé game.
↑ Course on combinatorial games in finite model theory by Phokion Kolaitis (.ps file)
↑ Neil Immerman (1999). Descriptive complexity. Springer. ISBN 978-0-387-98600-5. , chapter 6

Grädel, Erich; Kolaitis, Phokion G.; Libkin, Leonid; Maarten, Marx; Spencer, Joel; Vardi, Moshe Y.; Venema, Yde; Weinstein, Scott (2007). Finite model theory and its applications. Texts in Theoretical Computer Science. An EATCS Series. Berlin: Springer-Verlag. ISBN 978-3-540-00428-8. Zbl 1133.03001.

External links