Dynkin system

A Dynkin system, named after Eugene Dynkin, is a collection of subsets of another universal set 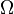$\Omega$ satisfying a set of axioms weaker than those of σ-algebra. Dynkin systems are sometimes referred to as λ-systems (Dynkin himself used this term) or d-system.^[1] These set families have applications in measure theory and probability.

The primary relevance of λ-systems are their use in applications of the π-λ theorem.

Definitions

Let Ω be a nonempty set, and let $D$ be a collection of subsets of Ω (i.e., $D$ is a subset of the power set of Ω). Then $D$ is a Dynkin system if

Ω ∈ $D$ ,
if A, B ∈ $D$ and A ⊆ B, then B \ A ∈ $D$ ,
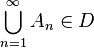if A₁, A₂, A₃, ... is a sequence of subsets in $D$ and A_n ⊆ A_n+1 for all n ≥ 1, then $\bigcup_{n=1}^\infty A_n\in D$ .

Equivalently, $D$ is a Dynkin system if

Ω ∈ $D$ ,
if A ∈ D, then A^c ∈ D,
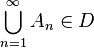if A₁, A₂, A₃, ... is a sequence of subsets in $D$ such that A_i ∩ A_j = Ø for all i ≠ j, then $\bigcup_{n=1}^\infty A_n\in D$ .

The second definition is generally preferred as it usually is easier to check.

An important fact is that a Dynkin system which is also a π-system (i.e., closed under finite intersection) is a σ-algebra. This can be verified by noting that condition 3 and closure under finite intersection implies closure under countable unions.

Given any collection 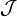$\mathcal{J}$ of subsets of 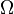$\Omega$ , there exists a unique Dynkin system denoted 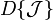$D\{\mathcal J\}$ which is minimal with respect to containing 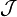$\mathcal J$ . That is, if 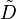$\tilde D$ is any Dynkin system containing 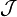$\mathcal J$ , then 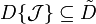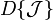$D\{\mathcal J\}\subseteq\tilde D$ . $D\{\mathcal J\}$ is called the Dynkin system generated by 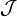$\mathcal{J}$ . Note 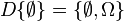$D\{\emptyset\}=\{\emptyset,\Omega\}$ . 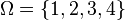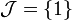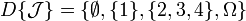For another example, let $\Omega=\{1,2,3,4\}$ and $\mathcal J=\{1\}$ ; then $D\{\mathcal J\}=\{\emptyset,\{1\},\{2,3,4\},\Omega\}$ .

Dynkin's π-λ theorem

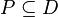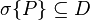If $P$ is a π-system and $D$ is a Dynkin system with $P\subseteq D$ , then $\sigma\{P\}\subseteq D$ . In other words, the σ-algebra generated by $P$ is contained in $D$ .

One application of Dynkin's π-λ theorem is the uniqueness of a measure that evaluates the length of an interval (known as the Lebesgue measure):

Let (Ω, B, λ) be the unit interval [0,1] with the Lebesgue measure on Borel sets. Let μ be another measure on Ω satisfying μ[(a,b)] = b − a, and let D be the family of sets S such that μ[S] = λ[S]. Let I = { (a,b),[a,b),(a,b],[a,b] : 0 < a ≤ b < 1 }, and observe that I is closed under finite intersections, that I ⊂ D, and that B is the σ-algebra generated by I. It may be shown that D satisfies the above conditions for a Dynkin-system. From Dynkin's π-λ Theorem it follows that D in fact includes all of B, which is equivalent to showing that the Lebesgue measure is unique on B.

Additional applications are in the article on π-systems.

Notes

↑ Charalambos Aliprantis, Kim C. Border (2006). Infinite Dimensional Analysis: a Hitchhiker's Guide, 3rd ed. Springer. Retrieved August 23, 2010.

References

Gut, Allan (2005). Probability: A Graduate Course. New York: Springer. doi:10.1007/b138932. ISBN 0-387-22833-0.
Billingsley, Patrick (1995). Probability and Measure. New York: John Wiley & Sons, Inc. ISBN 0-471-00710-2.
David Williams (2007). Probability with Martingales. Cambridge University Press. p. 193. ISBN 0-521-40605-6.

This article incorporates material from Dynkin system on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.