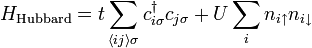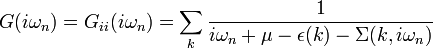Dynamical mean field theory

Dynamical mean-field theory (DMFT) is a method to determine the electronic structure of strongly correlated materials. In such materials, the approximation of independent electrons, which is used in density functional theory and usual band structure calculations, breaks down. Dynamical Mean-Field Theory, a non-perturbative treatment of local interactions between electrons, bridges the gap between the nearly free electron gas limit and the atomic limit of condensed-matter physics.^[1]

DMFT consists in mapping a many-body lattice problem to a many-body local problem, called an impurity model.^[2] While the lattice problem is in general intractable, the impurity model is usually solvable through various schemes. The mapping in itself does not constitute an approximation. The only approximation made in ordinary DMFT schemes is to assume the lattice self-energy to be a momentum-independent (local) quantity. This approximation becomes exact in the limit of lattices with an infinite coordination.^[3]

One of DMFT's main successes is to describe the phase transition between a metal and a Mott insulator when the strength of electronic correlations is increased. It has been successfully applied to real materials, in combination with the local density approximation of density functional theory.^[4]^[5]

Relation to mean-field theory

The DMFT treatment of lattice quantum models is similar to the mean-field theory (MFT) treatment of classical models such as the Ising model.^[6] In the Ising model, the lattice problem is mapped onto an effective single site problem, whose magnetization is to reproduce the lattice magnetization through an effective "mean-field". This condition is called the self-consistency condition. It stipulates that the single-site observables should reproduce the lattice "local" observables by means of an effective field. While the N-site Ising Hamiltonian is hard to solve analytically (to date, analytical solutions exist only for the 1D and 2D case), the single-site problem is easily solved.

Likewise, DMFT maps a lattice problem (e.g the Hubbard model) onto a single-site problem. In DMFT, the local observable is the local Green's function. Thus, the self-consistency condition for DMFT is for the impurity Green's function to reproduce the lattice local Green's function through an effective mean-field which, in DMFT, is the hybridization function $\Delta(\tau)$ of the impurity model. DMFT owes its name to the fact that the mean-field $\Delta(\tau)$ is time-dependent, or dynamical. This also points to the major difference between the Ising MFT and DMFT: Ising MFT maps the N-spin problem into a single-site, single-spin problem. DMFT maps the lattice problem onto a single-site problem, but the latter fundamentally remains a N-body problem which captures the temporal fluctuations due to electron-electron correlations.

Description of DMFT for the Hubbard model

The DMFT mapping

Single-orbital Hubbard model

The Hubbard model ^[7] describes the onsite interaction between electrons of opposite spin by a single parameter, $U$ . The Hubbard Hamiltonian may take the following form:

H_{\text{Hubbard}}=t \sum_{\langle ij \rangle \sigma} c_{i\sigma}^{\dagger}c_{j\sigma} + U\sum_{i}n_{i \uparrow} n_{i\downarrow}

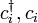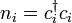where $c_i^{\dagger},c_i$ denote the creation and annihilation operators of an electron on a localized orbital on site $i$ , and $n_i=c_i^{\dagger}c_i$ .

The following assumptions have been made:

only one orbital contributes to the electronic properties (as might be the case of copper atoms in superconducting cuprates, whose $d$ -bands are non-degenerate),
the orbitals are so localized that only nearest-neighbor hopping $t$ is taken into account

The auxiliary problem: the Anderson impurity model

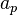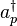The Hubbard model is in general intractable under usual perturbation expansion techniques. DMFT maps this lattice model onto the so-called Anderson impurity model (AIM). This model describes the interaction of one site (the impurity) with a "bath" of electronic levels (described by the annihilation and creation operators $a_p$ and $a_p^{\dagger}$ ) through a hybridization function. The Anderson model corresponding to our single-site model is a single-orbital Anderson impurity model, whose hamiltonian formulation is the following:

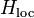H_{\text{AIM}}=\underbrace{\sum_{p}\epsilon_p a_p^{\dagger}a_p}_{H_{\text{bath}}} + \underbrace{\sum_{p\sigma}\left(V_{p}^{\sigma}c_{\sigma}^{\dagger}a_{p\sigma}+h.c.\right)}_{H_{\text{mix}}}+\underbrace{U n_{\uparrow} n_{\downarrow}-\mu \left(n_{\uparrow}+n_{\downarrow}\right)}_{H_{\text{loc}}}

where

$H_{\text{bath}}$ describes the non-correlated electronic levels $\epsilon_p$ of the bath
$H_{\text{loc}}$ describes the impurity, where two electrons interact with the energetical cost $U$
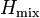$H_{\text{mix}}$ describes the hybridization (or coupling) between the impurity and the bath through hybridization terms $V_p^{\sigma}$

The Matsubara Green's function of this model, defined by 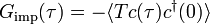$G_{\text{imp}}(\tau) = - \langle T c(\tau) c^{\dagger}(0)\rangle$ , is entirely determined by the parameters 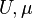$U,\mu$ and the so-called hybridization function 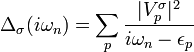$\Delta_\sigma(i\omega_n) = \sum_{p}\frac{|V_p^\sigma|^2}{i\omega_n-\epsilon_p}$ , which is the imaginary-time Fourier-transform of $\Delta_{\sigma}(\tau)$ .

This hybridization function describes the dynamics of electrons hopping in and out of the bath. It should reproduce the lattice dynamics such that the impurity Green's function is the same as the local lattice Green's function. It is related to the non-interacting Green's function by the relation:

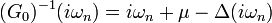(G_0)^{-1}(i\omega_n)=i\omega_n+\mu-\Delta(i\omega_n)

(1)

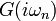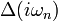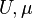Solving the Anderson impurity model consists in computing observables such as the interacting Green's function $G(i\omega_n)$ for a given hybridization function $\Delta(i\omega_n)$ and $U,\mu$ . It is a difficult but not intractable problem. There exists a number of ways to solve the AIM, such as

The Numerical renormalization group
Exact diagonalization
Iterative perturbation theory
Non-crossing approximation
Continuous-Time Quantum Monte Carlo algorithms^[8]^[9]^[10]^[11]^[12]

Self-consistency equations

The self-consistency condition requires the impurity Green's function 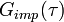$G_{imp}(\tau)$ to coincide with the local lattice Green's function $G_{ii}(\tau) = -\langle T c_i(\tau)c_i^{\dagger}(0)\rangle$ :

G(i\omega_n) = G_{ii}(i\omega_n) = \sum_k \frac {1}{i\omega_n +\mu - \epsilon(k) - \Sigma(k,i\omega_n)}

where $\Sigma(k,i\omega_n)$ denotes the lattice self-energy.

DMFT approximation: locality of the lattice self-energy

The only DMFT approximations (apart from the approximation that can be made in order to solve the Anderson model) consists in neglecting the spatial fluctuations of the lattice self-energy, by equating it to the impurity self-energy:

\Sigma(k,i\omega_n) \approx \Sigma_{imp}(i\omega_n)

This approximation becomes exact in the limit of lattices with infinite coordination, that is when the number of neighbors of each site is infinite. Indeed, one can show that in the diagrammatic expansion of the lattice self-energy, only local diagrams survive when one goes into the infinite coordination limit.

Thus, as in classical mean-field theories, DMFT is supposed to get more accurate as the dimensionality (and thus the number of neighbors) increases. Put differently, for low dimensions, spatial fluctuations will render the DMFT approximation less reliable.

The DMFT loop

In order to find the local lattice Green's function, one has to determine the hybridization function such that the corresponding impurity Green's function will coincide with the sought-after local lattice Green's function. An intuitive method would be the following: for a given $U$ , $\mu$ and temperature $T$

First, compute the non-interacting lattice Green's function 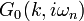$G_0(k,i\omega_n)$ , and extract its local part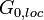 $G_{0,loc}$
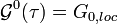
The self-consistency condition requires it to be equal to the impurity Green's function, $\mathcal{G}^0(\tau) = G_{0,loc}$
Compute the corresponding hybridization function through (1)
Solve the AIM for a new impurity Green's function 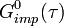$G_{imp}^0(\tau)$ , extract its self-energy: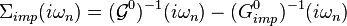 $\Sigma_{imp}(i\omega_n) = (\mathcal{G}^0)^{-1}(i\omega_n) - (G_{imp}^0)^{-1}(i\omega_n)$
Make the DMFT approximation: $\Sigma(k,i\omega_n) \approx \Sigma_{imp}(i\omega_n)$
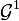
Compute the new lattice Green's function, extract its local part and go back to step 2 with a new $\mathcal{G}^1$

Self-consistency is reached when 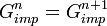$G_{imp}^n = G_{imp}^{n+1}$ .

Applications

The local lattice Green's function and other impurity observables can be used to calculate a number of physical quantities as a function of correlations $U$ , bandwidth, filling (chemical potential $\mu$ ), and temperature $T$ :

the spectral function (which gives the band structure)
the kinetic energy
the double occupancy of a site
response functions (compressibility, optical conductivity, specific heat)

In particular, the drop of the double-occupancy as $U$ increases is a signature of the Mott transition.

Extensions of DMFT

DMFT has several extensions, extending the above formalism to multi-orbital, multi-site problems.

Multi-orbital extension

DMFT can be extended to Hubbard models with multiple orbitals, namely with electron-electron interactions of the form 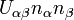$U_{\alpha \beta} n_{\alpha}n_{\beta}$ where $\alpha$ and $\beta$ denote different orbitals. This is especially relevant for compounds whose $d$ -orbitals are degenerate, such as iron in the newly discovered high-temperature iron-based superconductors (pnictides).

Cluster DMFT

In order to improve on the DMFT approximation, the Hubbard model can be mapped on a multi-site impurity (cluster) problem, which allows one to add some spatial dependence to the impurity self-energy. Clusters contain 4 to 8 sites at low T and up to 100 sites at high T.

Extended DMFT

DMFT can be applied to more general models such as the t-J model.

References and notes

↑ A. Georges, G. Kotliar, W. Krauth and M. Rozenberg et al. (1996). "Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions". Reviews of Modern Physics 68 (1): 13. Bibcode:1996RvMP...68...13G. doi:10.1103/RevModPhys.68.13.
↑ A. Georges and G.Kotliar (1992). "Hubbard model in infinite dimensions". Physical Review B 45 (12): 6479. Bibcode:1992PhRvB..45.6479G. doi:10.1103/PhysRevB.45.6479.
↑ W. Metzner and D. Vollhardt (1989). "Correlated Lattice Fermions in d = ∞ Dimensions". Physical Review Letters 62 (3): 324–327. Bibcode:1989PhRvL..62..324M. doi:10.1103/PhysRevLett.62.324.
↑ G. Kotliar, S. Y. Savrasov, K. Haule, V. S. Oudovenko, O. Parcollet, and C. A. Marianetti et al. (2006). "Electronic structure calculations with dynamical mean-field theory". Reviews of Modern Physics 78 (3): 865. arXiv:cond-mat/0511085. Bibcode:2006RvMP...78..865K. doi:10.1103/RevModPhys.78.865.
↑ D. Vollhardt (2012). "Dynamical mean-field theory for correlated electrons". Annalen der Physik 524 (1): 1–19. Bibcode:2012AnP...524....1V. doi:10.1002/andp.201100250.
↑ Antoine Georges (2004). "AIP Conference Proceedings". Lectures on the Physics of Highly Correlated Electron Systems VIII , American Institute of Physics Conference Proceedings Vol. 715 (715): 3–74. arXiv:cond-mat/0403123. doi:10.1063/1.1800733. |chapter= ignored (help)
↑ John Hubbard (1963). "Electron Correlations in Narrow Energy Bands". Proceedings of the Royal Society A 276 (1365): 238. Bibcode:1963RSPSA.276..238H. doi:10.1098/rspa.1963.0204.
↑ A. N. Rubtsov, V. V. Savkin, and A. I. Lichtenstein (2005). "Continuous-time quantum Monte Carlo method for fermions". Physical Review B 72 (3): 035122. arXiv:cond-mat/0411344. Bibcode:2005PhRvB..72c5122R. doi:10.1103/PhysRevB.72.035122.
↑ Philipp Werner, Armin Comanac, Luca de’ Medici, Matthias Troyer, and Andrew J. Millis (2006). "Continuous-Time Solver for Quantum Impurity Models". Physical Review Letters 97 (7): 076405. arXiv:cond-mat/0512727. Bibcode:2006PhRvL..97g6405W. doi:10.1103/PhysRevLett.97.076405.
↑ Werner, Philipp and Millis, Andrew J. (2006). "Hybridization expansion impurity solver: General formulation and application to Kondo lattice and two-orbital models". Physical Review B 74 (15): 155107. arXiv:cond-mat/0607136. Bibcode:2006PhRvB..74o5107W. doi:10.1103/PhysRevB.74.155107.
↑ K. Haule (2007). "Quantum Monte Carlo Impurity Solver for Cluster DMFT and Electronic Structure Calculations". Physical Review B 75: 155113. arXiv:cond-mat/0612172. Bibcode:2007PhRvB..75o5113H. doi:10.1103/PhysRevB.75.155113.
↑ Gull, Emanuel and Millis, Andrew J. and Lichtenstein, Alexander I. and Rubtsov, Alexey N. and Troyer, Matthias and Werner, Philipp (2011). "Continuous-time Monte~Carlo methods for quantum impurity models". Reviews of Modern Physics 83: 349. arXiv:1012.4474. Bibcode:2011RvMP...83..349G. doi:10.1103/RevModPhys.83.349.

External links

Strongly Correlated Materials: Insights From Dynamical Mean-Field Theory G. Kotliar and D. Vollhardt
Lecture notes on the LDA+DMFT approach to strongly correlated materials Eva Pavarini, Erik Koch, Dieter Vollhardt, and Alexander Lichtenstein (eds.)
Lecture notes DMFT at 25: Infinite Dimensions Eva Pavarini, Erik Koch, Dieter Vollhardt, and Alexander Lichtenstein (eds.)