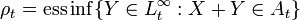Dynamic risk measure
In financial mathematics, a conditional risk measure is a random variable of the financial risk (particularly the downside risk) as if measured at some point in the future. A risk measure can be thought of as a conditional risk measure on the trivial sigma algebra.
A dynamic risk measure is a risk measure that deals with the question of how evaluations of risk at different times are related. It can be interpreted as a sequence of conditional risk measures. [1]
Conditional risk measure
A mapping 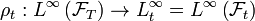 is a conditional risk measure if it has the following properties:
is a conditional risk measure if it has the following properties:
- Conditional cash invariance
-

- Monotonicity
-
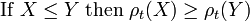
- Normalization
-
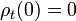
If it is a conditional convex risk measure then it will also have the property:
- Conditional convexity
-
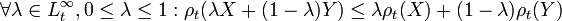
A conditional coherent risk measure is a conditional convex risk measure that additionally satisfies:
- Conditional positive homogeneity
-
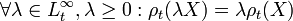
Acceptance set
The acceptance set at time  associated with a conditional risk measure is
associated with a conditional risk measure is
-
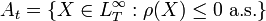 .
.
If you are given an acceptance set at time  then the corresponding conditional risk measure is
then the corresponding conditional risk measure is
where 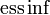 is the essential infimum.[2]
is the essential infimum.[2]
Regular property
A conditional risk measure 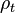 is said to be regular if for any
is said to be regular if for any 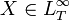 and
and 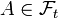 then
then 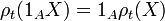 where
where 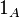 is the indicator function on
is the indicator function on  . Any normalized conditional convex risk measure is regular.[3]
. Any normalized conditional convex risk measure is regular.[3]
The financial interpretation of this states that the conditional risk at some future node (i.e. ![\rho_t(X)[\omega]](../I/m/119cd278d2897d8915ef497cd481f9d3.png) ) only depends on the possible states from that node. In a binomial model this would be akin to calculating the risk on the subtree branching off from the point in question.
) only depends on the possible states from that node. In a binomial model this would be akin to calculating the risk on the subtree branching off from the point in question.
Time consistent property
A dynamic risk measure is time consistent if and only if 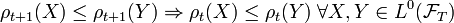 .[4]
.[4]
Example: dynamic superhedging price
The dynamic superhedging price has conditional risk measures of the form: ![\rho_t(-X) = \operatorname*{ess\sup}_{Q \in EMM} \mathbb{E}^Q[X | \mathcal{F}_t]](../I/m/36d40967fe5b09cff6ad374b57353895.png) . It is a widely shown result that this is also a time consistent risk measure.
. It is a widely shown result that this is also a time consistent risk measure.
References
- ↑ Acciaio, Beatrice; Penner, Irina (February 22, 2010). "Dynamic risk measures" (pdf). Retrieved July 22, 2010.
- ↑ Penner, Irina (2007). "Dynamic convex risk measures: time consistency, prudence, and sustainability" (pdf). Retrieved February 3, 2011.
- ↑ Detlefsen, K.; Scandolo, G. (2005). "Conditional and dynamic convex risk measures". Finance and Stochastics 9 (4): 539–561. doi:10.1007/s00780-005-0159-6.
- ↑ Cheridito, Patrick; Stadje, Mitja (October 2008). "Time-inconsistency of VaR and time-consistent alternatives".