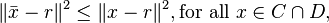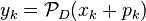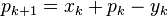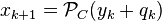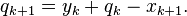Dykstra's projection algorithm
Dykstra's algorithm is a method that computes a point in the intersection of convex sets, and is a variant of the alternating projection method (also called the projections onto convex sets method). In its simplest form, the method finds a point in the intersection of two convex sets by iteratively projecting onto each of the convex set; it differs from the alternating projection method in that there are intermediate steps. A parallel version of the algorithm was developed by Gaffke and Mathar.
The method is named after R. L. Dykstra who proposed it in the 1980s.
A key difference between Dykstra's algorithm and the standard alternating projection method occurs when there is more than one point in the intersection of the two sets. In this case, the alternating projection method gives some arbitrary point in this intersection, whereas Dykstra's algorithm gives a specific point: the projection of r onto the intersection, where r is the initial point used in the algorithm,
Algorithm
Dykstra's algorithm finds for each  the only
the only 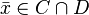 such that:
such that:
where 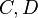 are convex sets. This problem is equivalent to finding the projection of
are convex sets. This problem is equivalent to finding the projection of  onto the set
onto the set 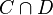 , which we denote by
, which we denote by 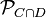 .
.
To use Dykstra's algorithm, one must know how to project onto the sets  and
and  separately.
separately.
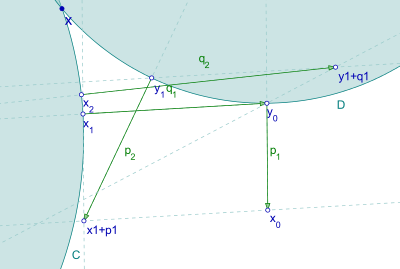
First, consider the basic alternating projection (aka POCS) method (first studied, in the case when the sets 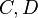 were linear subspaces, by John von Neumann[1]), which initializes
were linear subspaces, by John von Neumann[1]), which initializes 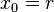 and then generates the sequence
and then generates the sequence
-
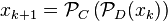 .
.
Dykstra's algorithm is of a similar form, but uses additional auxiliary variables. Start with 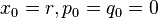 and update by
and update by
Then the sequence 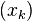 converges to the solution of the original problem. For convergence results and a modern perspective on the literature, see [2]
converges to the solution of the original problem. For convergence results and a modern perspective on the literature, see [2]
References
- Boyle, J. P.; Dykstra, R. L. (1986). "A method for finding projections onto the intersection of convex sets in Hilbert spaces". Lecture Notes in Statistics 37: 28–47. doi:10.1007/978-1-4613-9940-7_3.
- Gaffke, N.; Mathar, R. (1989). "A cyclic projection algorithm via duality". Metrika 36: 29–54. doi:10.1007/bf02614077.
- ↑ J. von Neumann, On rings of operators. Reduction theory, Ann. of Math. 50 (1949) 401–485 (a reprint of lecture notes first distributed in 1933).
- ↑ P. L. Combettes and J.-C. Pesquet, "Proximal splitting methods in signal processing," in: Fixed-Point Algorithms for Inverse Problems in Science and Engineering, (H. H. Bauschke, R. S. Burachik, P. L. Combettes, V. Elser, D. R. Luke, and H. Wolkowicz, Editors), pp. 185–212. Springer, New York, 2011