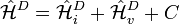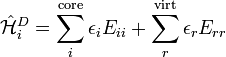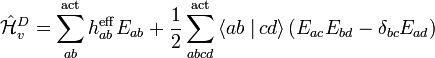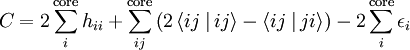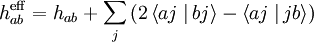Dyall Hamiltonian

In quantum chemistry, the Dyall Hamiltonian is a modified Hamiltonian with two-electron nature. It can be written as follows:

\hat{\mathcal{H}}^D = \hat{\mathcal{H}}^D_i + \hat{\mathcal{H}}^D_v + C

\hat{\mathcal{H}}^D_i = \sum_{i}^{\rm core} \epsilon_i E_{ii} + \sum_r^{\rm virt} \epsilon_r E_{rr}

\hat{\mathcal{H}}^D_v = \sum_{ab}^{\rm act} h_{ab}^{\rm eff} E_{ab} + \frac{1}{2} \sum_{abcd}^{\rm act} \left\langle ab \left.\right| cd \right\rangle \left(E_{ac} E_{bd} - \delta_{bc} E_{ad} \right)

C = 2 \sum_{i}^{\rm core} h_{ii} + \sum_{ij}^{\rm core} \left( 2 \left\langle ij \left.\right| ij\right\rangle - \left \langle ij \left.\right| ji\right\rangle \right) - 2 \sum_{i}^{\rm core} \epsilon_i

h_{ab}^{\rm eff} = h_{ab} + \sum_j \left( 2 \left\langle aj \left.\right| bj \right\rangle - \left\langle aj \left.\right| jb \right\rangle \right)

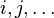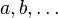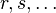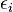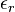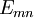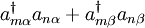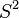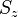where labels $i,j,\ldots$ , $a,b,\ldots$ , $r,s,\ldots$ denote core, active and virtual orbitals (see Complete active space) respectively, $\epsilon_i$ and $\epsilon_r$ are the orbital energies of the involved orbitals, and $E_{mn}$ operators are the spin-traced operators $a^{\dagger}_{m\alpha}a_{n\alpha} + a^{\dagger}_{m\beta}a_{n\beta}$ . These operators commute with $S^2$ and $S_z$ , therefore the application of these operators on a spin-pure function produces again a spin-pure function.

The Dyall Hamiltonian behaves like the true Hamiltonian inside the CAS space, having the same eigenvalues and eigenvectors of the true Hamiltonian projected onto the CAS space.