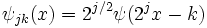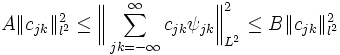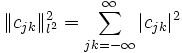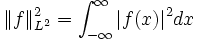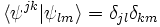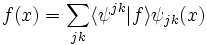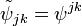Dual wavelet

In mathematics, a dual wavelet is the dual to a wavelet. In general, the wavelet series generated by a square integrable function will have a dual series, in the sense of the Riesz representation theorem. However, the dual series is not in general representable by a square integral function itself.

Definition

Given a square integrable function 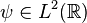\psi\in L^2(\mathbb{R}), define the series 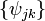\{\psi_{jk}\} by

\psi_{jk}(x) = 2^{j/2}\psi(2^jx-k)

for integers 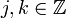j,k\in \mathbb{Z}.

Such a function is called an R-function if the linear span of 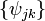\{\psi_{jk}\} is dense in 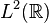L^2(\mathbb{R}), and if there exist positive constants A, B with 0<A\leq B < \infty such that

A \Vert c_{jk} \Vert^2_{l^2} \leq \bigg\Vert \sum_{jk=-\infty}^\infty c_{jk}\psi_{jk}\bigg\Vert^2_{L^2} \leq B \Vert c_{jk} \Vert^2_{l^2}\,

for all bi-infinite square summable series 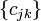\{c_{jk}\}. Here, 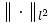\Vert \cdot \Vert_{l^2} denotes the square-sum norm:

\Vert c_{jk} \Vert^2_{l^2} = \sum_{jk=-\infty}^\infty \vert c_{jk}\vert^2

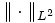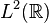and \Vert \cdot\Vert_{L^2} denotes the usual norm on L^2(\mathbb{R}):

\Vert f\Vert^2_{L^2}= \int_{-\infty}^\infty \vert f(x)\vert^2 dx

By the Riesz representation theorem, there exists a unique dual basis 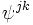\psi^{jk} such that

\langle \psi^{jk} \vert \psi_{lm} \rangle = \delta_{jl} \delta_{km}

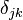where \delta_{jk} is the Kronecker delta and 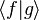\langle f\vert g \rangle is the usual inner product on 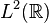L^2(\mathbb{R}). Indeed, there exists a unique series representation for a square integrable function f expressed in this basis:

f(x) = \sum_{jk} \langle \psi^{jk} \vert f \rangle \psi_{jk}(x)

If there exists a function 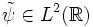\tilde{\psi} \in L^2(\mathbb{R}) such that

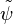\tilde{\psi}_{jk} = \psi^{jk}

then \tilde{\psi} is called the dual wavelet or the wavelet dual to ψ. In general, for some given R-function ψ, the dual will not exist. In the special case of 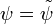\psi = \tilde{\psi}, the wavelet is said to be an orthogonal wavelet.

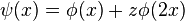An example of an R-function without a dual is easy to construct. Let \phi be an orthogonal wavelet. Then define \psi(x) = \phi(x) + z\phi(2x) for some complex number z. It is straightforward to show that this ψ does not have a wavelet dual.

See also

References