Dual representation

This article is about a mathematical concept. For the psychological concept, see Dual representation (psychology).

In mathematics, if $G$ is a group and $ρ$ is a linear representation of it on the vector space $V$ , then the dual representation $ρ*$ is defined over the dual vector space $V *$ as follows:^[1]

ρ*(g)

is the transpose of

ρ(g -1)

, that is,

ρ*(g)

ρ(g -1) T

for all

g \in G

The dual representation is also known as the contragredient representation.

If $g$ is a Lie algebra and $π$ is a representation of it on the vector space $V$ , then the dual representation $π*$ is defined over the dual vector space $V *$ as follows:^[2]

π*(X)

-π(X) T

for all

X \in g

In both cases, the dual representation is a representation in the usual sense.

Motivation

In representation theory, both vectors in $V$ and linear functionals in $V *$ are considered as column vectors so that the representation can act (by matrix multiplication) from the left. Given a basis for $V$ and the dual basis for $V *$ , the action of a linear functional $φ$ on $v$ , $φ(v)$ can be expressed by matrix multiplication,

\langle\varphi, v\rangle \equiv \varphi(v) = \varphi^Tv

where the superscript $T$ is matrix transpose. Consistency requires

\langle{\rho}^*(g)\varphi, \rho(g)v\rangle = \langle\varphi, v\rangle.

^[3]

With the definition given,

\langle{\rho}^*(g)\varphi, \rho(g)v\rangle = \langle\rho(g^{-1})^T\varphi, \rho(g)v\rangle = (\rho(g^{-1})^T\varphi)^T \rho(g)v = \varphi^T\rho(g^{-1})\rho(g)v = \varphi^Tv = \langle\varphi, v\rangle

For the Lie algebra representation one chooses consistency with a possible group representation. Generally, if $Π$ is a representation of a Lie group, then $π$ given by

\pi(X) = \frac{d}{dt}\Pi(e^{tX})|_{t = 0}.

is a representation of its Lie algebra. If $Π*$ is dual to $Π$ , then its corresponding Lie algebra representation $π*$ is given by

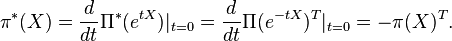\pi^*(X) = \frac{d}{dt}\Pi^*(e^{tX})|_{t = 0} = \frac{d}{dt}\Pi(e^{-tX})^T|_{t = 0} = -\pi(X)^T.

.^[4]

Generalization

A general ring module does not admit a dual representation. Modules of Hopf algebras do, however.

References

↑ Lecture 1 of Fulton, William; Harris, Joe (1991), Representation theory. A first course, Graduate Texts in Mathematics, Readings in Mathematics 129, New York: Springer-Verlag, ISBN 978-0-387-97495-8, MR 1153249, ISBN 978-0-387-97527-6
↑ Lecture 8 of Fulton, William; Harris, Joe (1991), Representation theory. A first course, Graduate Texts in Mathematics, Readings in Mathematics 129, New York: Springer-Verlag, ISBN 978-0-387-97495-8, MR 1153249, ISBN 978-0-387-97527-6
↑ Lecture 1, page 4 of Fulton, William; Harris, Joe (1991), Representation theory. A first course, Graduate Texts in Mathematics, Readings in Mathematics 129, New York: Springer-Verlag, ISBN 978-0-387-97495-8, MR 1153249, ISBN 978-0-387-97527-6
↑ Lecture 8, page 111 of Fulton, William; Harris, Joe (1991), Representation theory. A first course, Graduate Texts in Mathematics, Readings in Mathematics 129, New York: Springer-Verlag, ISBN 978-0-387-97495-8, MR 1153249, ISBN 978-0-387-97527-6

Dual representation

Motivation

Generalization

See also

References