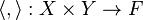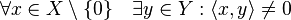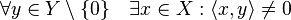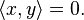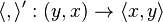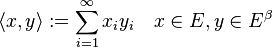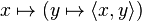Dual pair
In functional analysis and related areas of mathematics a dual pair or dual system is a pair of vector spaces with an associated bilinear map to the base field.
A common method in functional analysis, when studying normed vector spaces, is to analyze the relationship of the space to its continuous dual, the vector space of all possible continuous linear forms on the original space. A dual pair generalizes this concept to arbitrary vector spaces, with the duality being expressed as a bilinear map. Using the bilinear map, semi norms can be constructed to define a polar topology on the vector spaces and turn them into locally convex spaces, generalizations of normed vector spaces.
Definition
A dual pair[1] is a 3-tuple  consisting of two vector spaces
consisting of two vector spaces  and
and  over the same field
over the same field 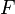 and a bilinear map
and a bilinear map
with
and
We call 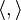 the duality pairing, and say that it puts
the duality pairing, and say that it puts  and
and  in duality.
in duality.
When the two spaces are a vector space  (or a module over a ring in general) and its dual
(or a module over a ring in general) and its dual 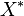 , we call the the canonical duality pairing
, we call the the canonical duality pairing 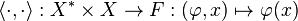 the natural pairing.
the natural pairing.
We call two elements 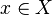 and
and 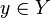 orthogonal if
orthogonal if
We call two sets 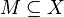 and
and 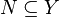 orthogonal if each pair of elements from
orthogonal if each pair of elements from  and
and  are orthogonal.
are orthogonal.
Example
A vector space  together with its algebraic dual
together with its algebraic dual 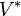 and the bilinear map defined as
and the bilinear map defined as
forms a dual pair.
A locally convex topological vector space space  together with its topological dual
together with its topological dual 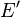 and the bilinear map defined as
and the bilinear map defined as
forms a dual pair. (To show this, the Hahn–Banach theorem is needed.)
For each dual pair  we can define a new dual pair
we can define a new dual pair 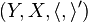 with
with
A sequence space  and its beta dual
and its beta dual 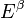 with the bilinear map defined as
with the bilinear map defined as
form a dual pair.
Comment
Associated with a dual pair  is an injective linear map from
is an injective linear map from  to
to 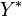 given by
given by
There is an analogous injective map from  to
to 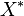 .
.
In particular, if either of  or
or  is finite-dimensional, these maps are isomorphisms.
is finite-dimensional, these maps are isomorphisms.