Dual of BCH is an independent source
A certain family of BCH codes have a particularly useful property, which is that
treated as linear operators, their dual operators turns their input into an 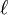 -wise independent source. That is, the set of vectors from the input vector space are mapped to an
-wise independent source. That is, the set of vectors from the input vector space are mapped to an 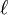 -wise independent source. The proof of this fact below as the following Lemma and Corollary is useful in derandomizing the algorithm for a
-wise independent source. The proof of this fact below as the following Lemma and Corollary is useful in derandomizing the algorithm for a  -approximation to MAXEkSAT.
-approximation to MAXEkSAT.
Lemma
Let  be a linear code such that
be a linear code such that  has distance greater than
has distance greater than 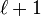 . Then
. Then  is an
is an 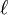 -wise independent source.
-wise independent source.
Proof of Lemma
It is sufficient to show that given any  matrix M, where k is greater than or equal to l, such that the rank of M is l, for all
matrix M, where k is greater than or equal to l, such that the rank of M is l, for all  ,
,  takes every value in
takes every value in  the same number of times.
the same number of times.
Since M has rank l, we can write M as two matrices of the same size, 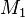 and
and 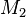 , where
, where 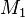 has rank equal to l. This means that
has rank equal to l. This means that  can be rewritten as
can be rewritten as  for some
for some  and
and 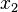 .
.
If we consider M written with respect to a basis where the first l rows are the identity matrix, then  has zeros wherever
has zeros wherever 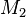 has nonzero rows, and
has nonzero rows, and 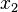 has zeros wherever
has zeros wherever 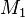 has nonzero rows.
has nonzero rows.
Now any value y, where  , can be written as
, can be written as  for some vectors
for some vectors 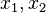 .
.
We can rewrite this as:

Fixing the value of the last  coordinates of
coordinates of
 (note that there are exactly
(note that there are exactly  such choices), we can rewrite this equation again as:
such choices), we can rewrite this equation again as:
 for some b.
for some b.
Since 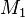 has rank equal to l, there
is exactly one solution
has rank equal to l, there
is exactly one solution  , so the total number of solutions is exactly
, so the total number of solutions is exactly  , proving the lemma.
, proving the lemma.
Corollary
Recall that BCH2,m,d is an ![[n=2^m, n-1 -\lceil {d-2}/2\rceil m, d]_2](../I/m/ca0deb043a07b79d71016aa1989af1f0.png) linear code.
linear code.
Let  be BCH2,log n,ℓ+1. Then
be BCH2,log n,ℓ+1. Then  is an
is an 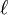 -wise independent source of size
-wise independent source of size 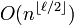 .
.
Proof of Corollary
The dimension d of C is just  . So
. So  .
.
So the cardinality of  considered as a set is just
considered as a set is just
 , proving the Corollary.
, proving the Corollary.