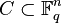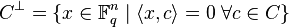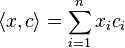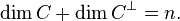Dual code

For players of both rugby codes, see List of dual-code rugby internationals.

In coding theory, the dual code of a linear code

C\subset\mathbb{F}_q^n

is the linear code defined by

C^\perp = \{x \in \mathbb{F}_q^n \mid \langle x,c\rangle = 0\;\forall c \in C \}

where

\langle x, c \rangle = \sum_{i=1}^n x_i c_i

is a scalar product. In linear algebra terms, the dual code is the annihilator of C with respect to the bilinear form <,>. The dimension of C and its dual always add up to the length n:

\dim C + \dim C^\perp = n.

A generator matrix for the dual code is a parity-check matrix for the original code and vice versa. The dual of the dual code is always the original code.

Self-dual codes

A self-dual code is one which is its own dual. This implies that n is even and dim C = n/2. If a self-dual code is such that each codeword's weight is a multiple of some constant 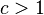c > 1, then it is of one of the following four types:[1]

Codes of types I, II, III, or IV exist only if the length n is a multiple of 2, 8, 4, or 2 respectively.

References

  1. ↑ Conway, J.H.; Sloane,N.J.A. (1988). Sphere packings, lattices and groups. Grundlehren der mathematischen Wissenschaften 290. Springer-Verlag. p. 77. ISBN 0-387-96617-X.
  • Hill, Raymond (1986). A first course in coding theory. Oxford Applied Mathematics and Computing Science Series. Oxford University Press. p. 67. ISBN 0-19-853803-0.
  • Pless, Vera (1982). Introduction to the theory of error-correcting codes. Wiley-Interscience Series in Discrete Mathematics. John Wiley & Sons. p. 8. ISBN 0-471-08684-3.
  • J.H. van Lint (1992). Introduction to Coding Theory. GTM 86 (2nd ed ed.). Springer-Verlag. p. 34. ISBN 3-540-54894-7.

External links