Dual-beta

In investing, dual-beta is a concept that states that a regular, market beta can be divided into downside beta and upside beta. Thus, dual stands for two betas, upside and downside. The fundamental principle behind dual-beta is that upside and downside betas are not the same. This is in contrast to what the Capital Asset Pricing Model assumes, which is that upside and downside betas are identical.[1]:617 Moreover, Fama and French (1992) demonstrated that beta is an imperfect measure of investment risk.[2]

Formula

The dual-beta model allows investors to differentiate downside risk – risk of loss – from upside risk, or gain. Regular beta fails to acknowledge, and thus to permit, this distinction. The dual-beta model does not assume that upside beta and downside betas are the same but actually calculates what the values are for the two betas, thus allowing investors to make better-informed investing decisions. “The dual-beta model can thus be expressed as:

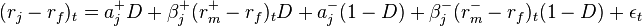
(r_j-r_f)_t = a_j^+D + \beta_j^+(r_m^+-r_f )_tD + a_j^-(1-D) + \beta_j^-(r_m^--r_f )_t(1-D) + \epsilon_t

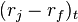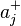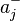where the dependent variable, (r_j-r_f)_t is the “the asset return in excess of the riskless rate, the two intercepts are a_j^+ and a_j^-, for the ‘up-market’ and ‘down-market’ regime respectively, and 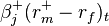\beta_j^+(r_m^+-r_f )_t is the product of the ‘up-market beta’ and the up-market excess return, and similarly 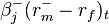\beta_j^- (r_m^--r_f )_t is the product of the ‘down-market beta’ and the down-market excess return.[3]:348 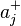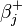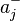a_j^+, \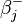beta_j^+, a_j^-, and \beta_j^- are the estimated parameters for up-market and down-market days, respectively; 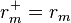r_m^+=r_m on days the market index did not decline and 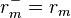r_m^-=r_m on days it did; 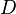D is a dummy variable, which takes the value of 1 when the market index daily return is non-negative and zero otherwise.”[1]:618 “The final term, 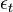\epsilon_t, reflects the idiosyncratic information not proportional to either the up-market or down-market excess returns.”[3]:348

Dual-Beta vs. Beta

Dual-beta can be a useful and an effective extension to traditional beta, which “underestimates equity risk about half the time, compared with the dual-beta estimate…which can translate into large differences in present value computations.”[3]:345 The dual-beta model is particularly useful because CAPM beta “consistently lags the dual-betas, in terms of average daily returns and return-to-standard deviation ratio.”[4]:71 Thus, investors can use the dual-beta approach to minimize their downside risk and maximize their upside risk/gain which cannot be achieved through the use of standard beta and the standard CAPM. While the dual-beta model has many benefits in terms of accuracy and usefulness, it might not be cost-effective for individual investors and is more suitable for financial planners due to transaction costs.[4]:80-81

See also

References

  1. ↑ 1.0 1.1 Chong, James; Halcoussis, Dennis; Phillips, Michael G. (September–October 2012). "Misleading Betas: An Educational Example". American Journal Of Business Education 5 (5). Retrieved 26 June 2013.
  2. ↑ Fama, Eugene F.; French, Kenneth (1992). "The Cross-Section of Expected Stock Returns". Journal of Finance 47 (2): 427–465. doi:10.2307/2329112.
  3. ↑ 3.0 3.1 3.2 Chong, James; Phillips, Michael G. (December 14, 2011). "Measuring risk for cost of capital: The downside beta approach". Journal of Corporate Treasury Management 4 (4). Retrieved 26 June 2013.
  4. ↑ 4.0 4.1 Chong, James, Ph.D.; Pfeiffer, Shaun, Ph.D.; Phillips, Michael G., Ph.D. (2011). "Can Dual Beta Filtering Improve Investor Performance". Journal of Personal Finance 10 (1). Retrieved 26 June 2013.

External links