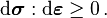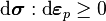Drucker stability
Drucker stability (also called the Drucker stability postulates) refers to a set of mathematical criteria that restrict the possible nonlinear stress-strain relations that can be satisfied by a solid material.[1] The postulates are named after Daniel C. Drucker. A material that does not satisfy these criteria is often found to be unstable in the sense that application of a load to a material point can lead to arbitrary deformations at that material point unless an additional length– or time–scale is specified in the constitutive relations.
The Drucker stability postulates are often invoked in nonlinear finite element analysis. Materials that satisfy these criteria are generally well-suited for numerical analysis, while materials that fail to satisfy this criterion are likely to present difficulties (i.e. non-uniqueness or singularity) during the solution process.
Drucker's first stability criterion
Drucker's first stability criterion (actually proposed by Rodney Hill and also called Hill's stability criterion[2]) is a strong condition on the incremental internal energy of a material which states that the incremental internal energy can only increase. The criterion may be written as follows:
Here, dσ is the stress increment tensor associated with the strain increment tensor dε through the constitutive relation.
Drucker's stability postulate
Drucker's postulate is applicable to elastic-plastic materials and states that in a cycle of plastic deformation the plastic work is always positive. This postulate can be expressed in incremental form as
where dεp is the incremental plastic strain tensor.
References
- ↑ Drucker, D.C. (1959), "A definition of a stable inelastic material", ASME Journal of Applied Mechanics 26: 101–195.
- ↑ Hill, R. (1958), "general theory of uniqueness and stability in elastic-plastic solids", Journal of the Mechanics and Physics of Solids 6: 236–249., doi:10.1016/0022-5096(58)90029-2