Double vector bundle
In mathematics, a double vector bundle is the combination of two compatible vector bundle structures, which contains in particular the double tangent 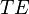 of a vector bundle
of a vector bundle  and the double tangent bundle
and the double tangent bundle 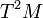 .
.
Definition and first consequences
A double vector bundle consists of 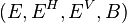 , where
, where
- the side bundles
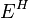 and
and 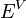 are vector bundles over the base
are vector bundles over the base  ,
, -
 is a vector bundle on both side bundles
is a vector bundle on both side bundles 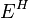 and
and 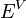 ,
, - the projection, the addition, the scalar multiplication and the zero map on E for both vector bundle structures are morphisms.
Double vector bundle morphism
A double vector bundle morphism (f_E, f_H, f_V, f_B) consists of maps 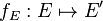 ,
, 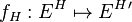 ,
, 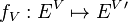 and
and 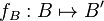 such that
such that 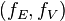 is a bundle morphism from
is a bundle morphism from 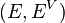 to
to 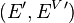 ,
, 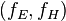 is a bundle morphism from
is a bundle morphism from 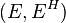 to
to 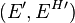 ,
, 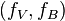 is a bundle morphism from
is a bundle morphism from 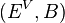 to
to 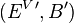 and
and 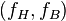 is a bundle morphism from
is a bundle morphism from 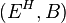 to
to 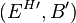 .
.
The 'flip of the double vector bundle 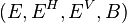 is the double vector bundle
is the double vector bundle 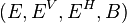 .
.
Examples
If  is a vector bundle over a differentiable manifold
is a vector bundle over a differentiable manifold  then
then 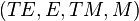 is a double vector bundle when considering its secondary vector bundle structure.
is a double vector bundle when considering its secondary vector bundle structure.
If  is a differentiable manifold, then its double tangent bundle
is a differentiable manifold, then its double tangent bundle 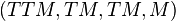 is a double vector bundle.
is a double vector bundle.
References
Mackenzie, K. (1992), "Double Lie algebroids and second-order geometry", Adv. Math. 94 (2): 180−239