Double (manifold)
In the subject of manifold theory in mathematics, if  is a manifold with boundary, its double is obtained by gluing two copies of
is a manifold with boundary, its double is obtained by gluing two copies of  together along their common boundary.[1] Precisely, the double is
together along their common boundary.[1] Precisely, the double is 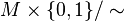 where
where 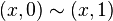 for all
for all 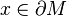 .
.
Although the concept makes sense for any manifold, and even for some non-manifold sets such as the Alexander horned sphere, the notion of double tends to be used primarily in the context that 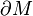 is non-empty and
is non-empty and  is compact.
is compact.
Doubles bound
Given a manifold  , the double of
, the double of  is the boundary of
is the boundary of ![M \times [0,1]](../I/m/8133e1a3347bba0eb3f5fa606d7e548f.png) . This gives doubles a special role in cobordism.
. This gives doubles a special role in cobordism.
Examples
The n-sphere is the double of the n-ball. In this context, the two balls would be the upper and lower hemi-sphere respectively. More generally, if  is closed, the double of
is closed, the double of 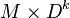 is
is 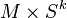 . Even more generally, the double of a disc bundle over a manifold is a sphere bundle over the same manifold. More concretely, the double of the Möbius strip is the Klein bottle.
. Even more generally, the double of a disc bundle over a manifold is a sphere bundle over the same manifold. More concretely, the double of the Möbius strip is the Klein bottle.
If  is a closed, oriented manifold and if
is a closed, oriented manifold and if 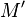 is obtained from
is obtained from  by removing an open ball, then the connected sum
by removing an open ball, then the connected sum 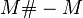 is the double of
is the double of 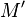 .
.
The double of a Mazur manifold is a homotopy 4-sphere.[2]
References
- ↑ Lee, John (2012), Introduction to Smooth Manifolds, Graduate Texts in Mathematics 218, Springer, p. 226, ISBN 9781441999825.
- ↑ Aitchison, I. R.; Rubinstein, J. H. (1984), "Fibered knots and involutions on homotopy spheres", Four-manifold theory (Durham, N.H., 1982), Contemp. Math. 35, Amer. Math. Soc., Providence, RI, pp. 1–74, doi:10.1090/conm/035/780575, MR 780575. See in particular p. 24.