Doob's martingale convergence theorems
In mathematics – specifically, in stochastic analysis – Doob's martingale convergence theorems are a collection of results on the long-time limits of supermartingales, named after the American mathematician Joseph L. Doob.
Statement of the theorems
In the following, (Ω, F, F∗, P), F∗ = (Ft)t≥0, will be a filtered probability space and N : [0, +∞) × Ω → R will be a right-continuous supermartingale with respect to the filtration F∗; in other words, for all 0 ≤ s ≤ t < +∞,
Doob's first martingale convergence theorem
Doob's first martingale convergence theorem provides a sufficient condition for the random variables Nt to have a limit as t → +∞ in a pointwise sense, i.e. for each ω in the sample space Ω individually.
For t ≥ 0, let Nt− = max(−Nt, 0) and suppose that
Then the pointwise limit
exists finite for P-almost all ω ∈ Ω.
Doob's second martingale convergence theorem
It is important to note that the convergence in Doob's first martingale convergence theorem is pointwise, not uniform, and is unrelated to convergence in mean square, or indeed in any Lp space. In order to obtain convergence in L1 (i.e., convergence in mean), one requires uniform integrability of the random variables Nt. By Chebyshev's inequality, convergence in L1 implies convergence in probability and convergence in distribution.
The following are equivalent:
- (Nt)t>0 is uniformly integrable, i.e.
- there exists an integrable random variable N ∈ L1(Ω, P; R) such that Nt → N as t → +∞ both P-almost surely and in L1(Ω, P; R), i.e.
Corollary: convergence theorem for continuous martingales
Let M : [0, +∞) × Ω → R be a continuous martingale such that
for some p > 1. Then there exists a random variable M ∈ Lp(Ω, P; R) such that Mt → M as t → +∞ both P-almost surely and in Lp(Ω, P; R).
Discrete-time results
Similar results can be obtained for discrete-time supermartingales and submartingales, the obvious difference being that no continuity assumptions are required. For example, the result above becomes
Let M : N × Ω → R be a discrete-time martingale such that
for some p > 1. Then there exists a random variable M ∈ Lp(Ω, P; R) such that Mk → M as k → +∞ both P-almost surely and in Lp(Ω, P; R)
Convergence of conditional expectations: Lévy's zero–one law
Doob's martingale convergence theorems imply that conditional expectations also have a convergence property.
Let (Ω, F, P) be a probability space and let X be a random variable in L1. Let F∗ = (Fk)k∈N be any filtration of F, and define F∞ to be the minimal σ-algebra generated by (Fk)k∈N. Then
both P-almost surely and in L1.
This result is usually called Lévy's zero–one law. The reason for the name is that if A is an event in F∞, then the theorem says that ![\mathbf{P}[ A | F_{k} ] \to \mathbf{1}_A](../I/m/c22c324f9dc6bc2c46aa147e95f744e8.png) almost surely, i.e., the limit of the probabilities is 0 or 1. In plain language, if we are learning gradually all the information that determines the outcome of an event, then we will become gradually certain what the outcome will be. This sounds almost like a tautology, but the result is still non-trivial. For instance, it easily implies Kolmogorov's zero–one law, since it says that for any tail event A, we must have
almost surely, i.e., the limit of the probabilities is 0 or 1. In plain language, if we are learning gradually all the information that determines the outcome of an event, then we will become gradually certain what the outcome will be. This sounds almost like a tautology, but the result is still non-trivial. For instance, it easily implies Kolmogorov's zero–one law, since it says that for any tail event A, we must have ![\mathbf{P}[ A ] = \mathbf{1}_A](../I/m/c5e8db25148b17be613e5ea099bc02de.png) almost surely, hence
almost surely, hence ![\mathbf{P}[ A ]\in\{0,1\}](../I/m/69f86813b0c1e26474beb5503602fc8b.png) .
.
See also
- Backwards martingale convergence theorem
References
- Øksendal, Bernt K. (2003). Stochastic Differential Equations: An Introduction with Applications (Sixth ed.). Berlin: Springer. ISBN 3-540-04758-1. (See Appendix C)
- Durrett, Rick (1996). Probability: theory and examples (Second ed.). Duxbury Press. ISBN 978-0-534-24318-0.
![N_{s} \geq \mathbf{E} \big[ N_{t} \big| F_{s} \big].](../I/m/b74bf1e78ef03b810b4b782e3dde725b.png)
![\sup_{t > 0} \mathbf{E} \big[ N_{t}^{-} \big] < + \infty.](../I/m/a73b2504414efb0a4f37ecd6524ba39f.png)
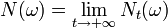

![\mathbf{E} \big[ \big| N_{t} - N \big| \big] = \int_{\Omega} \big| N_{t} (\omega) - N (\omega) \big| \, \mathrm{d} \mathbf{P} (\omega) \to 0 \mbox{ as } t \to + \infty.](../I/m/f6db8a8d1d60cd7c0293229b5ea7e58c.png)
![\sup_{t > 0} \mathbf{E} \big[ \big| M_{t} \big|^{p} \big] < + \infty](../I/m/26e1f9038d6427aa27b0450a5302f641.png)
![\sup_{k \in \mathbf{N}} \mathbf{E} \big[ \big| M_{k} \big|^{p} \big] < + \infty](../I/m/087acbec521d66b20190e10a43a005a7.png)
![\mathbf{E} \big[ X \big| F_{k} \big] \to \mathbf{E} \big[ X \big| F_{\infty} \big] \mbox{ as } k \to \infty](../I/m/2fe83ab34b99c0435eaf0f25e8e0e86e.png)