Dodd-Bullough-Mikhailov equation
Dodd-Bullough-Mikhailov equation is a nonlinear partial differential equation introduced by Roger Dodd, Robin Bullough, and Alexander Mikhailov[1]。
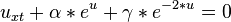
In 2005 Mathematician Wazwar combined the Tzitzeica equation with Dodd-Bullough-Mikhailov equation into Tzitz´eica-Dodd-Bullough-Mikhailov equation.[2]
Dodd-Bullough-Mikhailov equation has traveling wave solutions.
Analytic solution
Like Tzitzeica equation,the analytic solution of Dodd-Bullough-Mikhailov equation also as the general form of ln(f(a(bx+ct+d))), where a,b,c,d are arbitrary constants, and f is a trigonometric function.
Perform transformation:
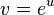 to transform Dodd-Bullough-Mikhailov equation into
to transform Dodd-Bullough-Mikhailov equation into
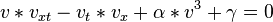
obtain the traveling wave solutions of v(x,t):
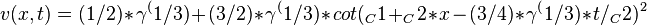
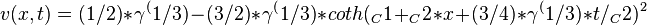
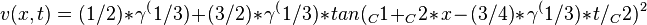
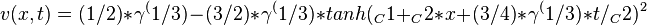
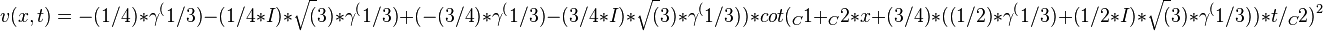
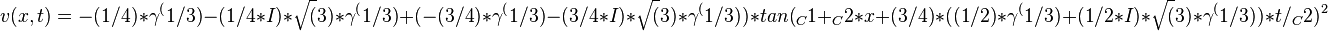
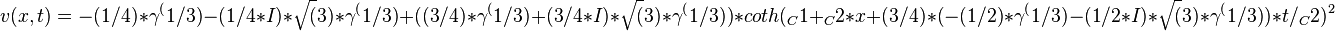
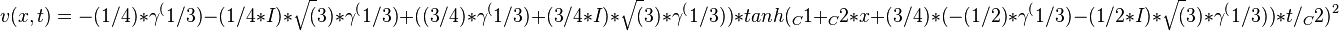
Then apply the inverse transform
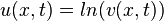
to get the traveling wave solutions of Dodd-Bullough-Mikhailov equation:
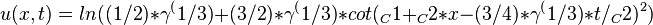
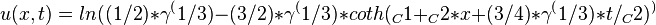
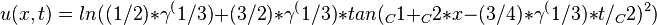
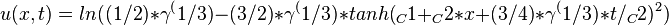
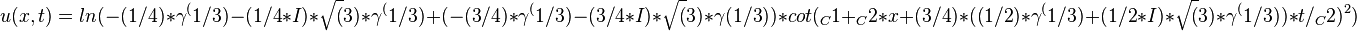
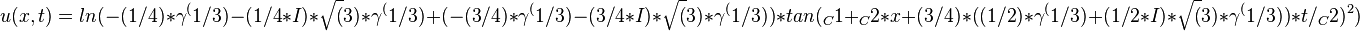
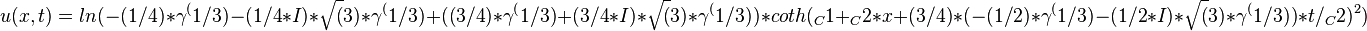
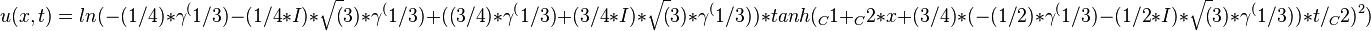
Traveling wave plot
The above solutions when plotted graphically provides a visual image of wave forms, they appear as complicated waves traveling from left to right.Some waves are periodic, some are solitary,called soliton.[3]
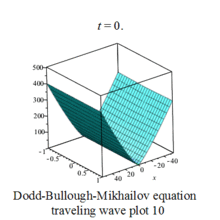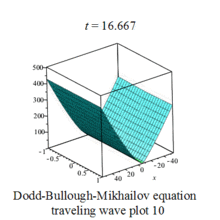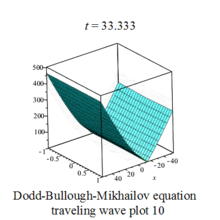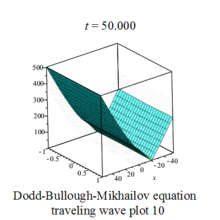 Dodd-Bullough-Mikhailov equation traveling wave plot |
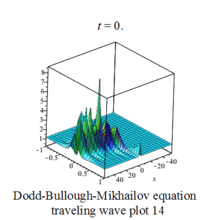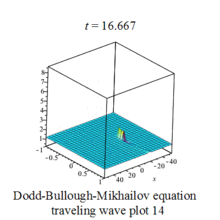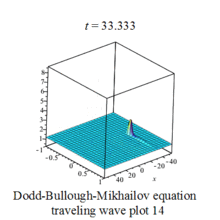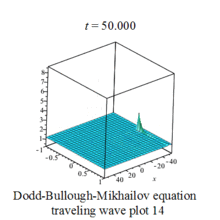 Dodd-Bullough-Mikhailov equation traveling wave plot |
 Dodd-Bullough-Mikhailov equation traveling wave plot |
 Dodd-Bullough-Mikhailov equation traveling wave plot |
 Dodd-Bullough-Mikhailov equation traveling wave plot |
 Dodd-Bullough-Mikhailov equation traveling wave plot |
 Dodd-Bullough-Mikhailov equation traveling wave plot |
 Dodd-Bullough-Mikhailov equation traveling wave plot |
 Dodd-Bullough-Mikhailov equation traveling wave plot |
 Dodd-Bullough-Mikhailov equation traveling wave plot |
 Dodd-Bullough-Mikhailov equation traveling wave plot |
 Dodd-Bullough-Mikhailov equation traveling wave plot |
 Dodd-Bullough-Mikhailov equation traveling wave plot |
 Dodd-Bullough-Mikhailov equation traveling wave plot |
References
- ↑ 李志斌编著 《非线性数学物理方程的行波解》 第105-107页,科学出版社 2008(Chinese)
- ↑ A.-M. Wazwaz, “The tanh method: solitons and periodic solutions for the Dodd-Bullough-Mikhailov and the Tzitz´eica- Dodd-Bullough equations,” Chaos, Solitons and Fractals, vol. 25,no. 1, pp. 55–63, 2005.
- ↑ A.-M. Wazwaz, “The tanh method: solitons and periodic solutions for the Dodd-Bullough-Mikhailov and the Tzitz´eica-Dodd-Bullough equations,” Chaos, Solitons and Fractals, vol. 25,no. 1, pp. 55–63, 2005.
- Graham W. Griffiths William E.Shiesser Traveling Wave Analysis of Partial Differential p135 Equations Academy Press
- Richard H. Enns George C. McCGuire, Nonlinear Physics Birkhauser,1997
- Inna Shingareva, Carlos Lizárraga-Celaya,Solving Nonlinear Partial Differential Equations with Maple Springer.
- Eryk Infeld and George Rowlands,Nonlinear Waves,Solitons and Chaos,Cambridge 2000
- Saber Elaydi,An Introduction to Difference Equationns, Springer 2000
- Dongming Wang, Elimination Practice,Imperial College Press 2004
- David Betounes, Partial Differential Equations for Computational Science: With Maple and Vector Analysis Springer, 1998 ISBN 9780387983004
- George Articolo Partial Differential Equations & Boundary Value Problems with Maple V Academic Press 1998 ISBN 9780120644759