Divided domain

In algebra, a divided domain is an integral domain R in which every prime ideal 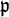\mathfrak{p} satisfies 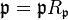\mathfrak{p} = \mathfrak{p} R_\mathfrak{p}. A locally divided domain is an integral domain that is a divided domain at every maximal ideal. A Prüfer domain is a basic example of a locally divided domain.[1] Divided domains were introduced by Akiba (1967) who called them AV-domains.

See also

References

  1. ↑ http://downloads.hindawi.com/journals/ijmms/1981/108278.pdf