Distributed lag
In statistics and econometrics, a distributed lag model is a model for time series data in which a regression equation is used to predict current values of a dependent variable based on both the current values of an explanatory variable and the lagged (past period) values of this explanatory variable.[1][2]
The starting point for a distributed lag model is an assumed structure of the form
or the form
where yt is the value at time period t of the dependent variable y, a is the intercept term to be estimated, and wi is called the lag weight (also to be estimated) placed on the value i periods previously of the explanatory variable x. In the first equation, the dependent variable is assumed to be affected by values of the independent variable arbitrarily far in the past, so the number of lag weights is infinite and the model is called an infinite distributed lag model. In the alternative, second, equation, there are only a finite number of lag weights, indicating an assumption that there is a maximum lag beyond which values of the independent variable do not affect the dependent variable; a model based on this assumption is called a finite distributed lag model.
In an infinite distributed lag model, an infinite number of lag weights need to be estimated; clearly this can be done only if some structure is assumed for the relation between the various lag weights, with the entire infinitude of them expressible in terms of a finite number of assumed underlying parameters. In a finite distributed lag model, the parameters could be directly estimated by ordinary least squares (assuming the number of data points sufficiently exceeds the number of lag weights); nevertheless, such estimation may give very imprecise results due to extreme multicollinearity among the various lagged values of the independent variable, so again it may be necessary to assume some structure for the relation between the various lag weights.
The concept of distributed lag models easily generalizes to the context of more than one right-side explanatory variable.
Unstructured estimation
The simplest way to estimate parameters associated with distributed lags is by ordinary least squares, assuming a fixed maximum lag  , assuming independent and identically distributed errors, and imposing no structure on the relationship of the coefficients of the lagged explanators with each other. However, multicollinearity among the lagged explanators often arises, leading to high variance of the coefficient estimates.
, assuming independent and identically distributed errors, and imposing no structure on the relationship of the coefficients of the lagged explanators with each other. However, multicollinearity among the lagged explanators often arises, leading to high variance of the coefficient estimates.
Structured estimation
Structured distributed lag models come in two types: finite and infinite. Infinite distributed lags allow the value of the independent variable at a particular time to influence the dependent variable infinitely far into the future, or to put it another way, they allow the current value of the dependent variable to be influenced by values of the independent variable that occurred infinitely long ago; but beyond some lag length the effects taper off toward zero. Finite distributed lags allow for the independent variable at a particular time to influence the dependent variable for only a finite number of periods.
Finite distributed lags
The most important structured finite distributed lag model is the Almon lag model.[3] This model allows the data to determine the shape of the lag structure, but the researcher must specify the maximum lag length; an incorrectly specified maximum lag length can distort the shape of the estimated lag structure as well as the cumulative effect of the independent variable. The Almon lag assumes that k+1 lag weights are related to n+1 linearly estimable underlying parameters (n<k) aj according to
for 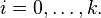
Infinite distributed lags
The most common type of structured infinite distributed lag model is the geometric lag, also known as the Koyck lag. In this lag structure, the weights (magnitudes of influence) of the lagged independent variable values decline exponentially with the length of the lag; while the shape of the lag structure is thus fully imposed by the choice of this technique, the rate of decline as well as the overall magnitude of effect are determined by the data. Specification of the regression equation is very straightforward: one includes as explanators (right-hand side variables in the regression) the one-period-lagged value of the dependent variable and the current value of the independent variable:
where 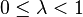 . In this model, the short-run (same-period) effect of a unit change in the independent variable is the value of b, while the long-run (cumulative) effect of a sustained unit change in the independent variable can be shown to be
. In this model, the short-run (same-period) effect of a unit change in the independent variable is the value of b, while the long-run (cumulative) effect of a sustained unit change in the independent variable can be shown to be
Other infinite distributed lag models have been proposed to allow the data to determine the shape of the lag structure. The polynomial inverse lag[4][5] assumes that the lag weights are related to underlying, linearly estimable parameters aj according to
for 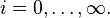
The geometric combination lag[6] assumes that the lags weights are related to underlying, linearly estimable parameters aj according to either
for 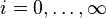 or
or
for 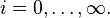
The gamma lag[7] and the rational lag[8] are other infinite distributed lag structures.
See also
- ARMAX
- Mixed data sampling
References
- ↑ Jeff B. Cromwell, et al., 1994. Multivariate Tests For Time Series Models. SAGE Publications, Inc. ISBN 0-8039-5440-9
- ↑ Judge, George, et al., 1980. The Theory and Practice of Econometrics. Wiley Publ.
- ↑ Almon, Shirley, "The distributed lag between capital appropriations and net expenditures," Econometrica 33, 1965, 178-196.
- ↑ Mitchell, Douglas W., and Speaker, Paul J., "A simple, flexible distributed lag technique: the polynomial inverse lag," Journal of Econometrics 31, 1986, 329-340.
- ↑ Gelles, Gregory M., and Mitchell, Douglas W., "An approximation theorem for the polynomial inverse lag," Economics Letters 30, 1989, 129-132.
- ↑ Speaker, Paul J., Mitchell, Douglas W., and Gelles, Gregory M., "Geometric combination lags as flexible infinite distributed lag estimators," Journal of Economic Dynamics and Control 13, 1989, 171-185.
- ↑ Schmidt, Peter, "A modification of the Almon distributed lag," Journal of the American Statistical Association 69, 1974, 679-681.
- ↑ Jorgenson, Dale W., "Rational distributed lag functions," Econometrica 34, 1966, 135-149.
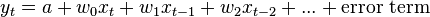
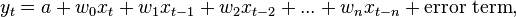
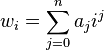
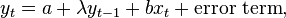
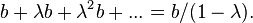
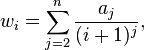
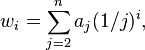
![w_i = \sum_{j=1}^{n} a_j [j/(n+1)]^i,](../I/m/8ccf003eb801463c95ad6a50b3da9337.png)