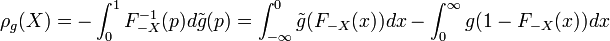Distortion risk measure
In financial mathematics, a distortion risk measure is a type of risk measure which is related to the cumulative distribution function of the return of a financial portfolio.
Mathematical definition
The function 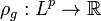 associated with the distortion function
associated with the distortion function ![g: [0,1] \to [0,1]](../I/m/97fd26d67e9595db275d4a69efc1fd5b.png) is a distortion risk measure if for any random variable of gains
is a distortion risk measure if for any random variable of gains 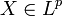 (where
(where 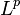 is the Lp space) then
is the Lp space) then
where 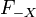 is the cumulative distribution function for
is the cumulative distribution function for 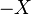 and
and 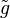 is the dual distortion function
is the dual distortion function 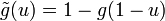 .[1]
.[1]
If 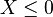 almost surely then
almost surely then 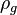 is given by the Choquet integral, i.e.
is given by the Choquet integral, i.e. 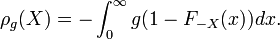 [1][2] Equivalently,
[1][2] Equivalently, ![\rho_g(X) = \mathbb{E}^{\mathbb{Q}}[-X]](../I/m/fed48379d0bf8034811a644153174ab5.png) [2] such that
[2] such that 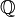 is the probability measure generated by
is the probability measure generated by  , i.e. for any
, i.e. for any 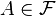 the sigma-algebra then
the sigma-algebra then 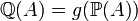 .[3]
.[3]
Properties
In addition to the properties of general risk measures, distortion risk measures also have:
- Law invariant: If the distribution of
 and
and  are the same then
are the same then 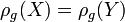 .
. - Monotone with respect to first order stochastic dominance.
- If
 is a concave distortion function, then
is a concave distortion function, then 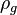 is monotone with respect to second order stochastic dominance.
is monotone with respect to second order stochastic dominance.
- If
-
 is a concave distortion function if and only if
is a concave distortion function if and only if 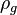 is a coherent risk measure.[1][2]
is a coherent risk measure.[1][2]
Examples
- Value at risk is a distortion risk measure with associated distortion function
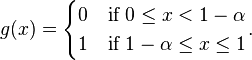 [2][3]
[2][3] - Conditional value at risk is a distortion risk measure with associated distortion function
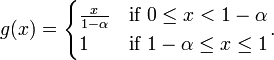 [2][3]
[2][3] - The negative expectation is a distortion risk measure with associated distortion function
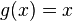 .[1]
.[1]
See also
References
- ↑ 1.0 1.1 1.2 1.3 Sereda, E. N.; Bronshtein, E. M.; Rachev, S. T.; Fabozzi, F. J.; Sun, W.; Stoyanov, S. V. (2010). "Distortion Risk Measures in Portfolio Optimization". Handbook of Portfolio Construction. p. 649. doi:10.1007/978-0-387-77439-8_25. ISBN 978-0-387-77438-1.
- ↑ 2.0 2.1 2.2 2.3 2.4 Julia L. Wirch; Mary R. Hardy. "Distortion Risk Measures: Coherence and Stochastic Dominance" (pdf). Retrieved March 10, 2012.
- ↑ 3.0 3.1 3.2 Balbás, A.; Garrido, J.; Mayoral, S. (2008). "Properties of Distortion Risk Measures". Methodology and Computing in Applied Probability 11 (3): 385. doi:10.1007/s11009-008-9089-z.
- Wu, Xianyi; Xian Zhou (April 7, 2006). "A new characterization of distortion premiums via countable additivity for comonotonic risks". Insurance: Mathematics and Economics 38 (2): 324–334. doi:10.1016/j.insmatheco.2005.09.002. Retrieved March 14, 2012.