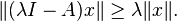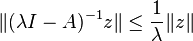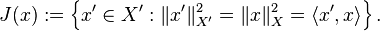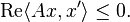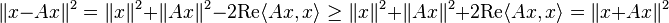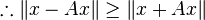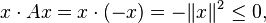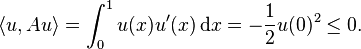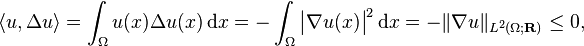Dissipative operator

In mathematics, a dissipative operator is a linear operator A defined on a linear subspace D(A) of Banach space X, taking values in X such that for all λ > 0 and all x ∈ D(A)

\|(\lambda I-A)x\|\geq\lambda\|x\|.

A couple of equivalent definitions are given below. A dissipative operator is called maximally dissipative if it is dissipative and for all λ > 0 the operator λI − A is surjective, meaning that the range when applied to the domain D is the whole of the space X.

An operator that obeys a similar condition but with a plus sign instead of a minus sign (that is, the negation of a dissipative operator) is called an accretive operator.^[1]

The main importance of dissipative operators is their appearance in the Lumer–Phillips theorem which characterizes maximally dissipative operators as the generators of contraction semigroups.

Properties

A dissipative operator has the following properties^[2]

From the inequality given above, we see that for any x in the domain of A, if ‖x‖ ≠ 0 then 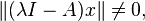$\|(\lambda I-A)x\|\ne 0,$ so the kernel of λI − A is just the zero vector and λI − A is therefore injective and has an inverse for all λ > 0. (If we have the strict inequality 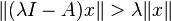$\|(\lambda I-A)x\|>\lambda\|x\|$ for all non-null x in the domain, then, by the triangle inequality, 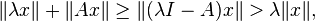$\|\lambda x\|+\|Ax\|\ge\|(\lambda I-A)x\|>\lambda\|x\|,$ which implies that A itself has an inverse.) We may then state that

\|(\lambda I-A)^{-1}z\|\leq\frac{1}{\lambda}\|z\|

for all z in the range of λI − A. This is the same inequality as that given at the beginning of this article, with

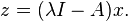z=(\lambda I-A)x.

(We could equally well write these as

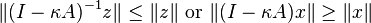\|(I-\kappa A)^{-1}z\|\leq\|z\|\text{ or }\|(I-\kappa A)x\|\geq\|x\|

which must hold for any positive κ.)

λI − A is surjective for some λ > 0 if and only if it is surjective for all λ > 0. (This is the aforementioned maximally dissipative case.) In that case one has (0, ∞) ⊂ ρ(A) (the resolvent set of A).
A is a closed operator if and only if the range of λI - A is closed for some (equivalently: for all) λ > 0.

Equivalent characterizations

Define the duality set of x ∈ X, a subset of the dual space X' of X, by

J(x):=\left\{x'\in X':\|x'\|_{X'}^2=\|x\|_{X}^2=\langle x',x\rangle \right\}.

By the Hahn–Banach theorem this set is nonempty.^[3] If X is reflexive, then J(x) consists of a single element. In the Hilbert space case (using the canonical duality between a Hilbert space and its dual) it consists of the single element x.^[4] Using this notation, A is dissipative if and only if^[5] for all x ∈ D(A) there exists a x' ∈ J(x) such that

{\rm Re}\langle Ax,x'\rangle\leq0.

In the case of Hilbert spaces, this becomes 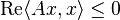${\rm Re}\langle Ax,x\rangle\leq0$ for all x in D(A). Since this is non-positive, we have

\|x-Ax\|^2=\|x\|^2+\|Ax\|^2-2{\rm Re}\langle Ax,x\rangle\geq\|x\|^2+\|Ax\|^2+2{\rm Re}\langle Ax,x\rangle=\|x+Ax\|^2

\therefore\|x-Ax\|\geq\|x+Ax\|

Since I−A has an inverse, this implies that 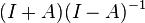$(I+A)(I-A)^{-1}$ is a contraction, and more generally, 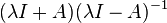$(\lambda I+A)(\lambda I-A)^{-1}$ is a contraction for any positive λ. The utility of this formulation is that if this operator is a contraction for some positive λ then A is dissipative. It is not necessary to show that it is a contraction for all positive λ (though this is true), in contrast to (λI−A)⁻¹ which must be proved to be a contraction for all positive values of λ.

Examples

For a simple finite-dimensional example, consider n-dimensional Euclidean space Rⁿ with its usual dot product. If A denotes the negative of the identity operator, defined on all of Rⁿ, then

x \cdot A x = x \cdot (-x) = - \| x \|^{2} \leq 0,

so A is a dissipative operator.

So long as the domain of an operator A (a matrix) is the whole Euclidean space, then it is dissipative if and only if A+A^* (the sum of A and its adjoint) does not have any positive eigenvalue, and (consequently) all such operators are maximally dissipative. (This criterion follows from the fact that the real part of 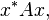$x^{*}Ax,$ which must be nonpositive for any x, is 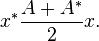$x^{*}\frac{A+A^{*}}2x.$ The eigenvalues of this quadratic form must therefore be nonpositive.) An equivalent condition is that for some (and hence any) positive 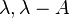$\lambda, \lambda-A$ has an inverse and the operator 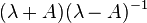$(\lambda+A)(\lambda-A)^{-1}$ is a contraction (that is, it either diminishes or leaves unchanged the norm of its operand). If the time derivative of a point x in the space is given by Ax, then the time evolution is governed by a contraction semigroup that constantly decreases the norm (or at least doesn't allow it to increase). (Note however that if the domain of A is a proper subspace, then A cannot be maximally dissipative because the range will not have a high enough dimensionality.)

Consider H = L²([0, 1]; R) with its usual inner product, and let Au = u′ with domain D(A) equal to those functions u in the Sobolev space H¹([0, 1]; R) with u(1) = 0. D(A) is dense in L²([0, 1]; R). Moreover, for every u in D(A), using integration by parts,

\langle u, A u \rangle = \int_{0}^{1} u(x) u'(x) \, \mathrm{d} x = - \frac1{2} u(0)^{2} \leq 0.

Hence, A is a dissipative operator. Furthermore, since there is a solution in D to

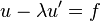u-\lambda u'=f

for any f in H, the operator A is maximally dissipative. Note that in a case of infinite dimensionality like this, the range can be the whole Banach space even though the domain is only a proper subspace thereof.

Consider H = H₀²(Ω; R) (see Sobolev space) for an open and connected domain Ω ⊆ Rⁿ and let A = Δ, the Laplace operator, defined on the dense subspace of compactly supported smooth functions on Ω. Then, using integration by parts,

\langle u, \Delta u \rangle = \int_\Omega u(x) \Delta u(x) \, \mathrm{d} x = - \int_\Omega \big| \nabla u(x) \big|^{2} \, \mathrm{d} x = - \| \nabla u \|_{L^{2} (\Omega; \mathbf{R})} \leq 0,

so the Laplacian is a dissipative operator.

Notes

↑ "Dissipative operator". Encyclopedia of Mathematics.
↑ Engel and Nagel Proposition II.3.14
↑ The theorem implies that for a given x there exists a continuous linear functional φ with the property that φ(x)=‖x‖, with the norm of φ equal to 1. We identify ‖x‖φ with x'.
↑ Engel and Nagel Exercise II.3.25i
↑ Engel and Nagel Proposition II.3.23

References

Engel, Klaus-Jochen; Nagel, Rainer (2000). One-parameter semigroups for linear evolution equations. Springer.
Renardy, Michael and Rogers, Robert C. (2004). An introduction to partial differential equations. Texts in Applied Mathematics 13 (Second ed.). New York: Springer-Verlag. p. 356. ISBN 0-387-00444-0. (Definition 12.25)