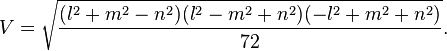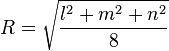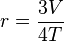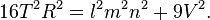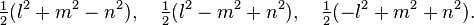Disphenoid


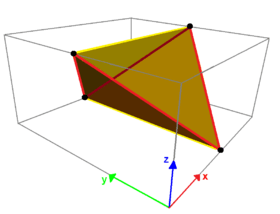
The tetragonal and digonal disphenoids can be positioned inside a cuboid bisecting two opposite faces. The tetragonal form has Coxeter diagram . All four faces are isosceles triangles. Both have four equal edges going around the sides. The digonal has two sets of isosceles triangle faces, while the tetragonal form has four identical isosceles triangle faces.
A rhombic disphenoid has 4 congruent scalene triangle faces, and can fit diagonally inside of a cuboid. It has three sets of edge lengths, existing as opposite pairs.
It can be given Coxeter diagram as an alternation of a cuboid .

In geometry, a disphenoid (also bisphenoid) (from Greek sphenoeides, "wedgelike" [1]) is a tetrahedron whose four faces are congruent acute-angled triangles.[2] It can also be described as a tetrahedron in which every two edges that are opposite each other have equal lengths. Other names are isosceles tetrahedron and equifacial tetrahedron. They can also be seen as digonal antiprisms as an alternated quadrilateral prism. All the solid angles and vertex figures of a disphenoid are the same, and the sum of the face angles at each vertex is equal to two right angles. However, a disphenoid is not a regular polyhedron, because, in general, its faces are not regular polygons, and it is not edge-transitive .

Special cases and generalizations

Tetrahedral subgroup relations
Tetrahedral symmetries shown in tetrahedral diagrams

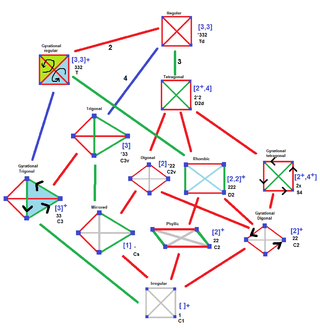
If the faces of a disphenoid are equilateral triangles, it is a regular tetrahedron with Td tetrahedral symmetry, although this is not normally called a disphenoid. The faces of a tetragonal disphenoid are identical isosceles, and it has D2d dihedral symmetry. The faces of a rhombic disphenoid are scalene and it has D2 dihedral symmetry. Tetragonal disphenoids and rhombic disphenoids are isohedra.

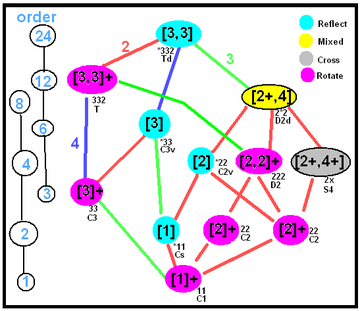
The digonal disphenoid is not a disphenoid as defined above. It has two sets of isosceles triangles faces, and it has C2v. The most general disphenoid term is the phyllic disphenoid with only two types of scalene triangles. Tetrahedral diagrams are included for each type below, with edges colored by isometric equivalence, and are gray colored for unique edges.

Name Edge
diagram		 Faces Symmetry
Schön. Coxeter Orb. Ord.
Regular tetrahedron
{3,3} or 4.( )		 Identical
equilateral triangles		 Td
T		[3,3]
[3,3]+
*332
332		24
12
Tetragonal disphenoid
2.{ }		 Identical
isosceles triangles		 D2d
S4		[2+,4]
[2+,4+]
2*2
2×		8
4
Rhombic disphenoid Identical
scalene triangles		 D2[2,2]+2224
Digonal disphenoid
{ }∨{ }		 Two equilateral and
two isosceles triangles		 C2v
C2		[2]
[2]+
*22
22		4
2
Two types of
isosceles triangles
Phyllic disphenoid C2[2]+ 22 2
Two types of
scalene triangles

Characterizations

A tetrahedron is a disphenoid if and only if its circumscribed parallelepiped is right-angled.[3]

We also have that a tetrahedron is a disphenoid if and only if the center in the circumscribed sphere and the inscribed sphere coincide.[4]

Another characterization states that if d1, d2 and d3 are the common perpendiculars of AB and CD; AC and BD; and AD and BC respectively in a tetrahedron ABCD, then the tetrahedron is a disphenoid if and only if d1, d2 and d3 are pairwise perpendicular.[3]

Metric formulas

The volume of a disphenoid with opposite edges of length l, m and n is given by[5]

V=\sqrt{\frac{(l^2+m^2-n^2)(l^2-m^2+n^2)(-l^2+m^2+n^2)}{72}}.

The circumscribed sphere has radius[5] (the circumradius)

R=\sqrt{\frac{l^2+m^2+n^2}{8}}

and the inscribed sphere has radius[5]

r=\frac{3V}{4T}

where V is the volume of the disphenoid and T is the area of any face, which is given by Heron's formula. There is also the following interesting relation connecting the volume and the circumradius:[5]

\displaystyle 16T^2R^2=l^2m^2n^2+9V^2.

The square of the lengths of the bimedians are[5]

\tfrac{1}{2}(l^2+m^2-n^2),\quad \tfrac{1}{2}(l^2-m^2+n^2),\quad \tfrac{1}{2}(-l^2+m^2+n^2).

Other properties

If the four faces of a tetrahedron have the same perimeter, then the tetrahedron is a disphenoid.[4]

If the four faces of a tetrahedron have the same area, then it is a disphenoid.[3] [4]

The centers in the circumscribed and inscribed spheres coincide with the centroid of the disphenoid.[5]

The bimedians are perpendicular to the edges they connect and to each other.[5]

Honeycombs and crystals

Some tetragonal disphenoids will form honeycombs. The disphenoid whose four vertices are (-1, 0, 0), (1, 0, 0), (0, 1, 1), and (0, 1, -1) is such a disphenoid.[6] Each of its four faces is an isosceles triangle with edges of lengths √3, √3, and 2. It can tesselate space to form the disphenoid tetrahedral honeycomb. As Gibb[7] describes, it can be folded without cutting or overlaps from a single sheet of a4 paper.

"Disphenoid" is also used to describe two forms of crystal:

See also

References

  1. ↑ Merriam-Webster Online Dictionary.
  2. ↑
    • Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. p. 15
  3. ↑ 3.0 3.1 3.2 Andreescu, Titu and Gelca, Razvan, "Mathematical Olympiad Challenges", Birkhäuser, second edition, 2009, pp. 30-31.
  4. ↑ 4.0 4.1 4.2 Brown, B. H., "Theorem of Bang. Isosceles tetrahedra", American Mathematical Monthly, April 1926, pp. 224-226.
  5. ↑ 5.0 5.1 5.2 5.3 5.4 5.5 5.6 Leech, John (1950), "Some properties of the isosceles tetrahedron", Mathematical Gazette 34 (310): 269–271.
  6. ↑ Coxeter, pp. 71–72; Senechal, Marjorie (1981). "Which tetrahedra fill space?". Mathematics Magazine 54 (5): 227–243. doi:10.2307/2689983. JSTOR 2689983.
  7. ↑ Gibb, William (1990). "Paper patterns: solid shapes from metric paper". Mathematics in School 19 (3): 2–4. Reprinted in Pritchard, Chris, ed. (2003). The Changing Shape of Geometry: Celebrating a Century of Geometry and Geometry Teaching. Cambridge University Press. pp. 363–366. ISBN 0-521-53162-4.

External links