Disk covering problem
The disk covering problem asks for the smallest real number 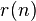 such that
such that  disks of radius
disks of radius 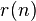 can be arranged in such a way as to cover the unit disk. Dually, for a given radius ε, one wishes to find the smallest integer n such that n disks of radius ε can cover the unit disk.[1]
can be arranged in such a way as to cover the unit disk. Dually, for a given radius ε, one wishes to find the smallest integer n such that n disks of radius ε can cover the unit disk.[1]
The best solutions to date are as follows:
| n | r(n) | Symmetry |
|---|---|---|
| 1 | 1 | All |
| 2 | 1 | All (2 stacked disks) |
| 3 | 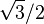 = 0.866025... = 0.866025... |
120°, 3 reflections |
| 4 | 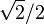 = 0.707107... = 0.707107... |
90°, 4 reflections |
| 5 | 0.609382... | 1 reflection |
| 6 | 0.555905... | 1 reflection |
| 7 | 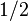 = 0.5 = 0.5 |
60°, 6 reflections |
| 8 | 0.445041... | ~51.4°, 7 reflections |
| 9 | 0.414213... | 45°, 8 reflections |
| 10 | 0.394930... | 36°, 9 reflections |
| 11 | 0.380083... | 1 reflection |
| 12 | 0.361141... | 120°, 3 reflections |
Method
This is the best known layout strategy for r(9) and r(10):
References
- ↑ Kershner, Richard (1939), "The number of circles covering a set", American Journal of Mathematics 61: 665–671, doi:10.2307/2371320, MR 0000043.
External links
- Weisstein, Eric W., "Disk Covering Problem", MathWorld.
- Finch, S. R. "Circular Coverage Constants." §2.2 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 484–489, 2003.
- Illustrations of circles covering circles