Disdyakis triacontahedron
| Disdyakis triacontahedron | |
|---|---|
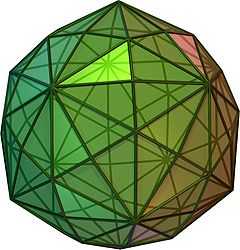 click for spinning version | |
| Type | Catalan |
| Conway notation | mD or dbD |
| Coxeter diagram | |
| Face polygon |  scalene triangle |
| Faces | 120 |
| Edges | 180 |
| Vertices | 62 = 12 + 20 + 30 |
| Face configuration | V4.6.10 |
| Symmetry group | Ih, H3, [5,3], (*532) |
| Rotation group | I, [5,3]+, (532) |
| Dihedral angle | 164° 53' 17" |
| Dual polyhedron | truncated icosidodecahedron |
| Properties | convex, face-transitive |
 Net | |
In geometry, a disdyakis triacontahedron, hexakis icosahedron or kisrhombic triacontahedron[1] is a Catalan solid with 120 faces and the dual to the Archimedean truncated icosidodecahedron. As such it is face uniform but with irregular face polygons. It looks a bit like an inflated rhombic triacontahedron—if one replaces each face of the rhombic triacontahedron with a single vertex and four triangles in a regular fashion one ends up with a disdyakis triacontahedron. That is, the disdyakis triacontahedron is the Kleetope of the rhombic triacontahedron. It also has the most faces among the Archimedean and Catalan solids, with the snub dodecahedron, with 92 faces, in second place.
If the bipyramids and the trapezohedra are excluded, the disdyakis triacontahedron has the most faces of any other strictly convex polyhedron where every face of the polyhedron has the same shape.
Symmetry
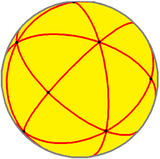
The edges of the polyhedron projected onto a sphere form 15 great circles, and represent all 15 mirror planes of reflective Ih icosahedral symmetry, as shown in this image. Combining pairs of light and dark triangles define the fundamental domains of the nonreflective (I) icosahedral symmetry. The edges of a compound of five octahedra also represent the 10 mirror planes of icosahedral symmetry.
 Disdyakis triacontahedron |
 Spherical disdyakis triacontahedron |
 Spherical compound of five octahedra |
Orthogonal projections
The disdyakis triacontahedron has three types of vertices which can be centered in orthogonally projection:
| Projective symmetry |
[2] | [6] | [10] |
|---|---|---|---|
| Image | 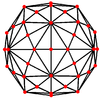 |
 |
 |
| Dual image |
 |
 |
 |
Related polyhedra
| Symmetry: [5,3], (*532) | [5,3]+, (532) | ||||||
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
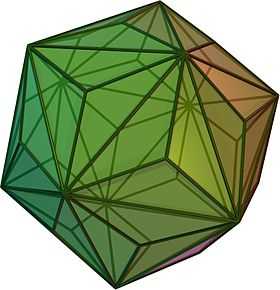
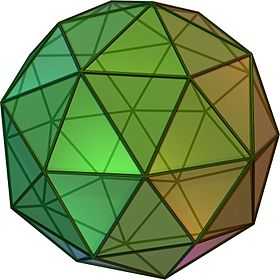
| {5,3} | t{5,3} | r{5,3} | 2t{5,3}=t{3,5} | 2r{5,3}={3,5} | rr{5,3} | tr{5,3} | sr{5,3} |
| Duals to uniform polyhedra | |||||||
 |
 |
 |
 |
 |
 | ||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
It is topologically related to a polyhedra sequence defined by the face configuration V4.6.2n. This group is special for having all even number of edges per vertex and form bisecting planes through the polyhedra and infinite lines in the plane, and continuing into the hyperbolic plane for any n ≥ 7.
With an even number of faces at every vertex, these polyhedra and tilings can be shown by alternating two colors so all adjacent faces have different colors.
Each face on these domains also corresponds to the fundamental domain of a symmetry group with order 2,3,n mirrors at each triangle face vertex.
| Sym. *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | Noncompact hyperbolic | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| *232 [2,3] D3h |
*332 [3,3] Td |
*432 [4,3] Oh |
*532 [5,3] Ih |
*632 [6,3] P6m |
*732 [7,3] |
*832 [8,3] |
*∞32 [∞,3] |
[12i,3] |
[9i,3] |
[6i,3] |
[3i,3] | |
| Figure |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| Schläfli | tr{2,3} | tr{3,3} | tr{4,3} | tr{5,3} | tr{6,3} | tr{7,3} | tr{8,3} | tr{∞,3} | tr{12i,3} | tr{9i,3} | tr{6i,3} | tr{3i,3} |
| Coxeter | ||||||||||||
| Dual figures | ||||||||||||
| Coxeter | ||||||||||||
| Duals |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Face | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
References
- ↑ Conway, Symmetries of things, p.284
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 730208 (The thirteen semiregular convex polyhedra and their duals, Page 25, Disdyakistriacontahedron )
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 285, kisRhombic triacontahedron )
External links
- Eric W. Weisstein, Disdyakis triacontahedron (Catalan solid) at MathWorld
- Disdyakis triacontahedron (Hexakis Icosahedron) – Interactive Polyhedron Model
| ||||||||||||||||||||||||||||||||||||