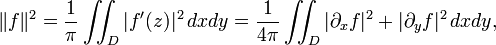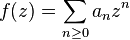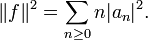Dirichlet space

In mathematics, the Dirichlet space is the Hilbert space of holomorphic functions defined on the unit disk D in the complex numbers for which the complex derivative is square integrable. The norm is given by the formula

\|f\|^2= {1\over \pi} \iint_D |f^\prime(z)|^2 \, dx dy = {1\over 4\pi}\iint_D |\partial_x f|^2 + |\partial_y f|^2 \, dx dy,

where the latter is the integral occurring in Dirichlet's principle for harmonic functions.

If

f(z) = \sum_{n\ge 0} a_n z^n

then

\|f\|^2 =\sum_{n\ge 0} n |a_n|^2.

Note that functions differing by a constant are identified.

References